Content
Compound
Planar Truss
Determinacy:
External Determinacy:
Internal Determinacy:
Compound Planar Truss
Besides the stability of a compound trusses, another important concern of a compound trusses is the determinacy.

Determinacy:
Although a compound truss is formed by joining two simple rigid trusses which are statically determinate togther, the compound truss can be statically indeterminate if the two simple rigid trusses is not properly connected or the compound truss is not properly constrained. In general, there are two concerns in the static determinacy of a truss. A truss should be internal statically determinate such that all forces in the truss member can be determined. And a truss should also be the external statically determinate such that all the external reactions can also be determined.
External Determinacy:
A truss is external statically deteminate when a truss is completely constrained with properly arranged supports and connections. By considering a truss as a rigid body structure in equilibrium, the number of equilibrium equation can be obtained is equal to three. In order to be external statically determinate, the number of unknown supporting reactions needed for the truss to be in equilibrium is equal to three.
When the supporting reactions is less than three, the truss becomes external unstable, althrough the unknown reactions may be determined. For example
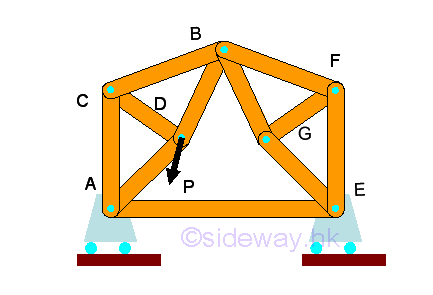
For the external statical indeterminacy of a truss, there are excess number of unknown supporting reactions for a rigid truss. For example R=4>3, the excess reaction is said to be redundant.
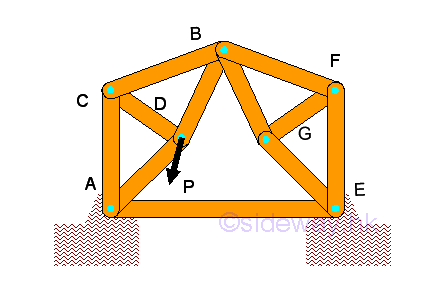
The excess number of unknown supporting reactions is only a necessary condition for external statical indeterminate. A truss with excess number of unknowns may also be determined in a collapsible compound truss. For example:
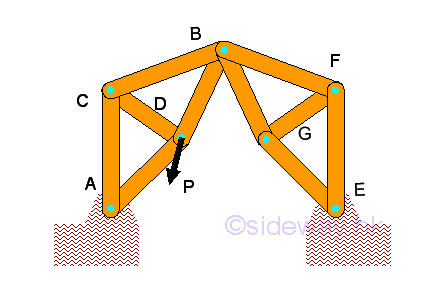
Internal Determinacy:
For a completely constrained rigid truss, the number of external unknown reaction is equal to three, the total number of unknwons is therefore equal to the number of force in truss members, m, plus the number of unknown reactions, R. And the number of equilibrium equations can be written from a truss with number of connecting joints, n, is equal to 2n. In order to be determinate, the number of unknowns should be equal to the number of equilibrium equations written from the connecting joints i.e. m+R=m+3=2n. In other words, the necessary condition of a compound truss to be statically determinate, rigid, and completely constrained is m=2n-3. And this also implies that all the unknown reactions and forces in all the truss members can be determined statically. However the connected truss members at the connected joint of a compound trusses is usually three or more truss members, the method of joints in general is not possible to determine the forces in all the truss members of the truss. As the compound trusses is statically determinate, all forces in truss members can be determined by solving all equilibrium equations written from connection joints simultaneously or by the method of section.
For example, a completely constrained rigid compound truss with 3 reactions, then m=2n-R imply 11=2(7)-3, therefore all unkown external reactions and all the forces in truss members can be determined by making use of the equilibrium equations, i.e. a properly completely constrained rigid compound truss is determinate.

For example, a constrained collapsible compound truss with 3 reactions, then m=2n-R imply 10<2(7)-3, therefore an improperly constrained collapsible compound truss is unstable.
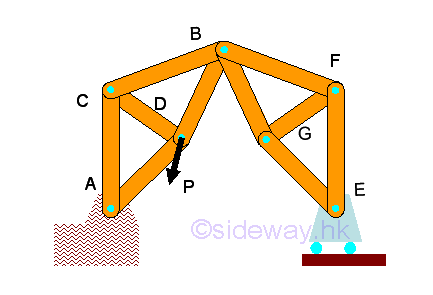
m=2n-R is only the necessary condition for a compound truss to be determinate becasue the truss member should be properly connected. For example, if more truss members are added, then m>=2n-R imply 13=2(8)-3, the geometric stability of the truss does not change, the truss will collapse under the applied force because the truss members added are not properly arranged.
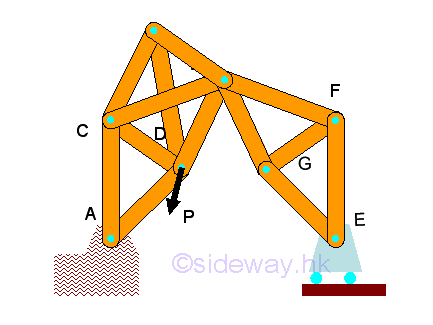
If the compound truss is completely constrained, when more truss members are added to a rigid truss, i.e. m>2n-R, the compound truss becomes overrigid. The excess truss member is said to be redundant. For example, a completely constrained rigid compound truss with 3 reactions, then m>2n-R imply 12>2(7)-3, the truss is overrigid, either one of the four members, AD, CD, DB, DE is said to be reduntant. Since the number of unknown forces in truss members is larger than the number of independent equilibrium equations obtained from the connecting joint, the compound truss is statically indeterminate.
©sideway
ID: 120300005 Last Updated: 3/6/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 31
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
