Compound Planar Truss

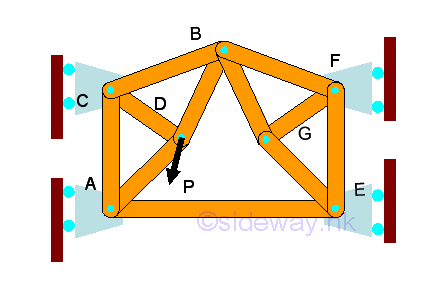
Sometimes simple truss are connected together to form a compound trusses which cannot be constructed through the method of simple truss construction.

Since the connected truss members at the connected joint of a compound trusses is usually three or more  truss members, the method of joints in general is not possible to determine the forces in all the truss members of the truss. As the compound trusses is statically determinate, all forces in truss members can be determined by solving all equilibrium equations written from connection joints simultaneously.

Besides there are also some trusses cannot be classified as either simple or compound trusses, these type of trusses are called complex trusses.

Stability:

Although a compound truss is formed by joining two simple rigid trusses togther, the compound truss can be unstable. In general, there are two concerns in the stability of a truss. A truss should be internal stable such that the truss does not change the shape of the truss after the truss is detached from the truss supports. And a truss should also be the external stabe such that the truss does not move under the applied forces.

Internal Stability:

A truss is internal instabe when the number and arrangement of members is sufficient enough to make the truss rigid. As in simple truss, all forces in the truss members of a stable truss should be in equilibrium after detaching from the truss supports. In order to determine all unknown forces in truss members, the number of equilibrium equations obtained from the connecting point should be equal to the number of unknown forces in truss members. Since the number of equilibrium equations can be obtained from the connecting joint is 2n and the number of reactions of a planar is equal to R=3, the number of unknown forces in truss members, m should be equal to m=2n-R=2n-3. The reactions R is used to constrain all the conntecting joints of the truss through constraining the truss members of the truss. And therefore the truss is internally unstable if the relationship between truss member and connecting joint is  m<2n-R=2n-3 because there are not enough reactions to constrain all the connecting joints of the truss and the structure will collapse. For example, if one truss member is removed, then m<2n-R imply 10<2(7)-3, the truss will collapse under the applied force because connecting joint c will move horizontally.

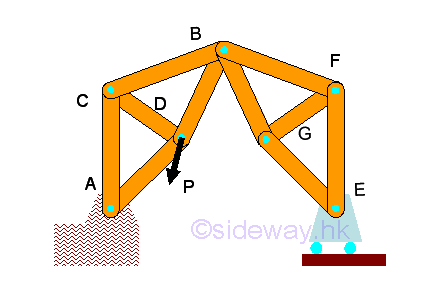
The necessary condition of the internal stability of a truss is m>=2n-R=2n-3. This condition only imply the truss can be internally stable or geometrically stable provided that the truss members are being properly arranged. For example, if more truss members are added, then m>=2n-R imply 13=2(8)-3, the geometric stability of the truss does not change, the truss will collapse under the applied force because the truss members added are not properly arranged.

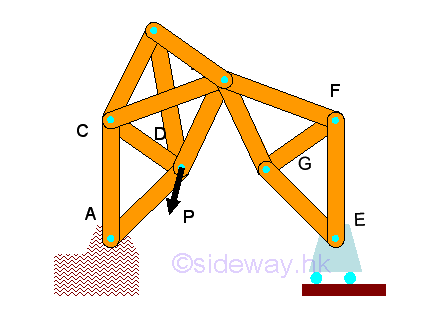
External Stability:

The external instability of a rigid truss is caused by the insufficient number or arrangement of external connections and supports. For example, a rigid truss with 2 reactions, then m<2n-R imply 11<2(7)-2, two reactions cannot constrain the truss from moving horizonally under the applied load

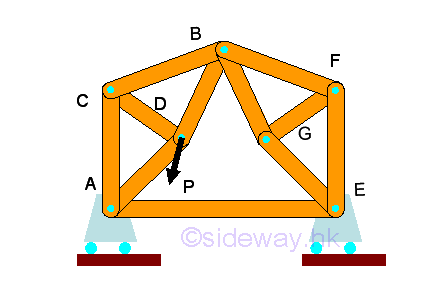
The necessary condition of the external stability of a truss is m>=2n-R=2n-3.  This condition only imply the truss can be externally stable provided that the truss are either being properly constrained or the truss is a rigid  uncollapsible structure.

As in internal stability of a truss, more reactions are needed to make the collapsible structure become rigid. For example, a fixed support is used to replace the roller support of the collapsible truss, then m>=2n-R imply 10>=2(7)-4,  for stopping the horizontal movement of joint E .

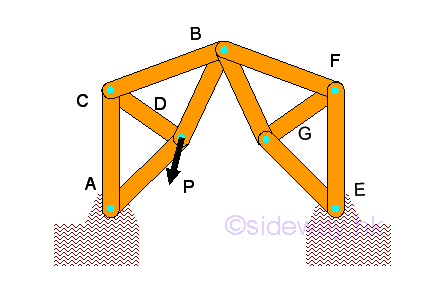
However, an external unstable truss can also have external connections and supports which are more than necessary when these external connections and supports are not properly constrained. For example, external connections and supports with either concurrent or parallel constraints then m>=2n-R imply 11>=2(7)-4, the truss can still move vertically.

Therefore a completely constrained truss should have sufficient number of supports which are arranged properly.

And a rigid truss should be both internally and externally stable.  The necessary condition of a rigid truss is  m>=2n-R.  And the external supports and connections should be properly constrained with no concurrent or parallel supports. Besides the truss should also not to be a collapsable truss