Content
Simple
Planar Truss
Characteristic of Forces in Simple Planar Trusses :
Condition of Unstable Boundary:
Zero-Force Members
and Reactions:
Forces in Truss:
Determinate of Forces at a joint:
Simple Planar Truss
Characteristic of Forces in Simple Planar Trusses :

Condition of Unstable Boundary:
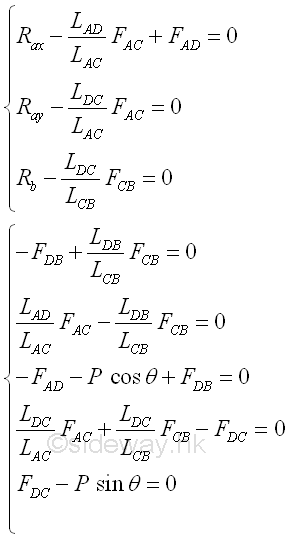
The eight equilibrium equations are independent equations for the eight unknowns including the three unknown boundaries. For a fully constarined truss, forces in members are the reactions due to the applied load and external reactions. The external reactions can therefore be represented by the corresponding forces in connected members accordingly. Considering only the five equilibrium equations without external reaction, there are five independent equations with five unknowns. The five equilibrium equations can be assembled into a 5X5 matrix. Imply
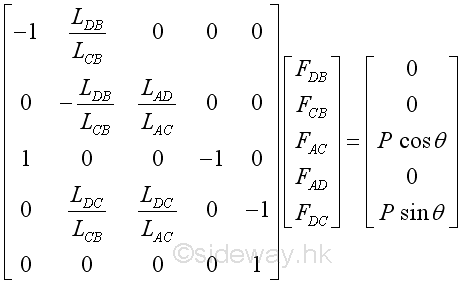
Since the five equations are linearly independent, the matrix is a nonsingular matrix and exactly one solution for the five unknown forces in members can be found. But for a non-fully constrained truss, the system of linear equations becomes either underdetermined or overdetermined. If a truss is partially constrained, the system of linear equations is overdetermined. In general, there is no unique solution with the exception that the extra equation is linearly dependent on the others.
Zero-Force Members and Reactions:
Following are the reactions on the supports and connections and forces in Truss members of the simple planar truss
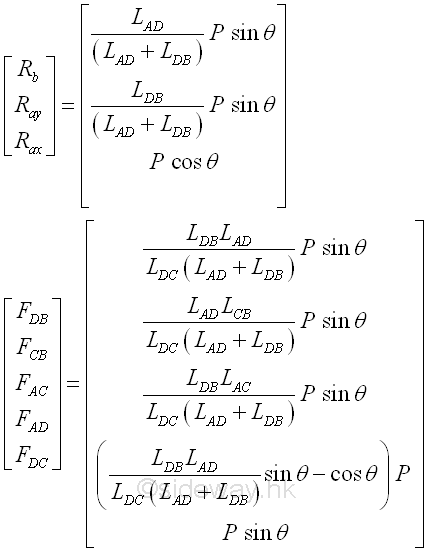
For a simple truss with a simple applied loading, the reactions are directly related to the lengths of the truss members and the angle of the applied load. For a vertical applied load, the horizontal reaction on the connection is equal to zero, i.e. cos θ=0. And the relationship between the two reactions is equal to the proportionality of the ratio of the reactions to the inverse ratio of their transverse displacements, truss member lengths, from the applied load. Imply
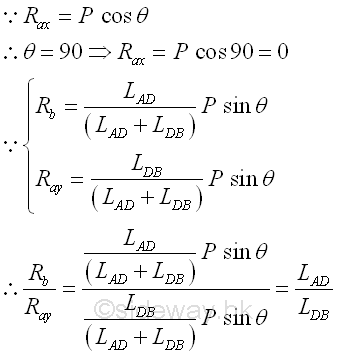
For a simple truss with a simple applied loading, the forces in truss memebers are also directly related to the lengths of the truss members and the angle of the applied load.
Since no moment is transmited at the joint pin, the applied load only alter the loading condition of the connected truss members directly along the axis of the truss member. Because the fixed horizontal constraint is located at A, and the horizontal boundary constraint at B is free, the horizontal component of the angle applied load can only alter the loading condition of the truss member AD. As in assumption, the truss member AD is in tension if the sense of the force is positive and the applied load points to left down with sense of negative. And the truss member AD can be a zero-force member when the applied load is applied at a specified angle according to the length of truss members. Imply

The vertical component of the applied load is completely transmitted by the truss member DC to the connecting joint pin C. The truss member DC is therefore always under tension and the magnitude is equal to the vertical component of the applied load. As in assumption, the truss member DC is in tension if the sense of the force is positive
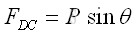
The vertical component of the applied load is then shared by truss members AC and CB at the connecting joint pin C to maintain the truss in upright position, and therefore truss members AC and CB are always under compression. As in assumption, the truss member AC and CB is in compression if the sense of the force is positive. And the relationship between the two forces in truss members AC and CB is equal to the proportionality of the ratio of the forces to the inverse ratio of the cosines of the angles formed by truss members with the horizontal axis. Imply
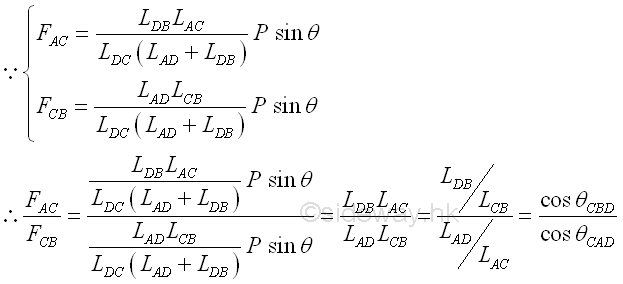
In general, the forces in truss members are not fixed values and are highly dependent on the applied locations and angles of the applied loads. Of course, forces in truss members are also changed with the truss construction design and the truss member dimension.
Forces in Truss:
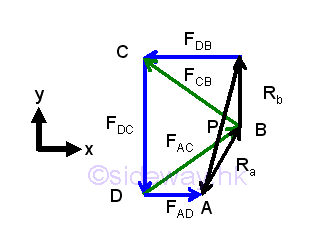
After constructing the single force diagram, a more clear picture of the forces in trusses is obtained. The applied load P is equal to the vector sum of reactions Ra and Rb. Since reaction Rb is always vertical, only the reaction Ra can react the change in the horizontal component of the applied load.
The vertical component of the applied load is transmitted to the truss through truss member DC. Therefore the force in truss member DC is equal to the vertical component of the applied load. The truss member DC is then supported by truss members AC and BC which enable the trusses to stand in an upright position. Therefore force in truss member DC is equal to the vector sum of the supporting forces in truss members AC and CB.
Truss members AD and DB are used to fix the other ends of truss members in order to make the trues rigid. Since the joint B is a free end, the force in truss member DB is only to maintain the truss member CB in a fixed position relative to the truss member DC.
The trapezoid formed by truss members DB, DC and AC, and reaction Rb. is fixed by the vertical component of applied load also. When the horizontal component of applied load is equal to zero, the reaction Ra becomes vertial, and the tensional forces in truss member DB and AD are equal. The tensional forces in truss member AD will increase if the horizontal component of the applied force further shift to right.
However, when the horizontal component of the applied force shift to the left and is equal to FDB , FAD will equal to zero according to the force vector diagram, The truss member AD becomes a zero-force member. The arctangent of FDC over FDB is equal to arctangent of truss members above, imply
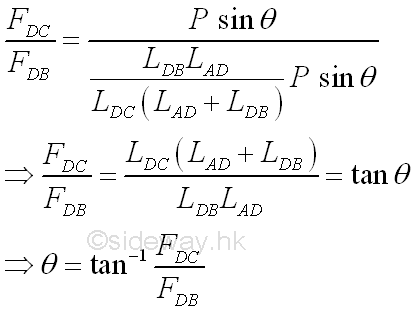
Therefore when the horizontal component of the applied force shift to the left further, the force in the truss member AD becomes negative, i.e. a compressive force.
Determinate of Forces at a joint:
When a truss joint is in equilibrium state, the resultant force at a joint must be equal to zero, therefore forces applied at a connecting joint may be determinate throught the application of force vector diagram.
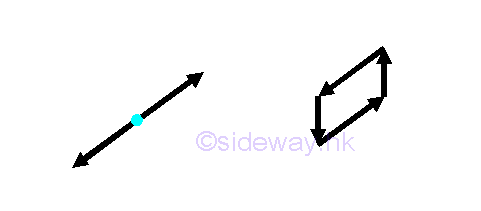
Simple truss members or forces at a point lying in straight lines, the forces in opposite truss member must be equal and opposite.
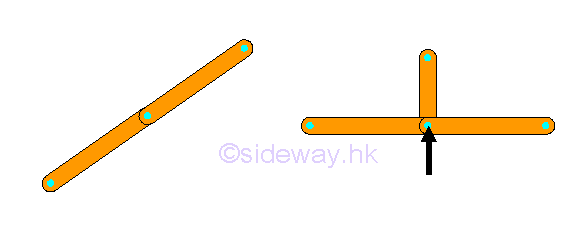
Or
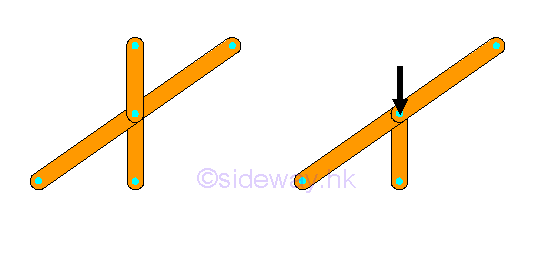
Because, the force vectors will form a closed force polygon or a balanced force vector pair.
Therefore in some cases, force in a truss member should be zero. For example, the force in the vertical truss member should be zero in order to be in equilibrium.
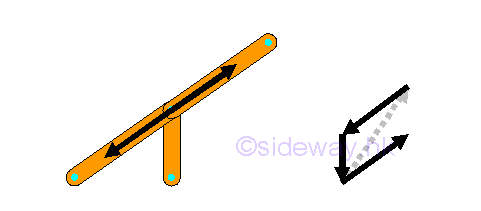
So, there are some impossible cases which should not be exist in the extire truss except both truss members are zero-force members.
©sideway
ID: 120200073 Last Updated: 3/20/2016 Revision: 1 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 31
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
