Content
Simple
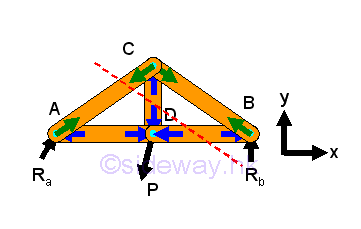
Planar Truss
Forces Analysis by Method of Sections:
Determination of Forces in Trusses :
Forces in Two Truss Members AD and AC:
Forces in Three Truss Members AC,
DC and CB:
Forces in Four Truss Members AC,
DC and CB:
Simple Planar Truss
Forces Analysis by Method of Sections:
The determination of forces in trusses by method of joints is limited by numbers of equations can be written from a joint. Mehod of joints can only work with two unknown forces because only two equilibrium equations can be written from a joint. And the determination of forces in trusses should start with joint with two unknowns only, Therefore the using of method of joint is usually used to determine of the forces in all truss member. When only one or a few forces in some of the truss members are interested, the most effective way is the using of method of sections.

For an equilibrium rigid body, every component parts of the rigid body should also be in equilibrium. The method of sections is the consideration of the rigid body into two sectional parts across truss members virtually. The main advantage of method of sections over method of joints is the numbers of equations can be written from a sectional part. When treating a sectional part as an equilibrium free rigid body, three equilibrium equations can be written from the sectional part.
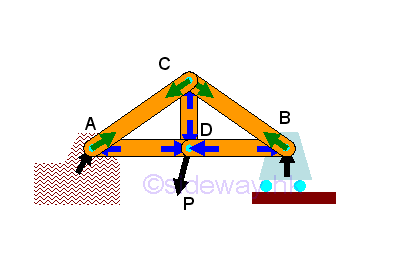
Therefore the key concept is to create a virtual section with maximum three unknowns only. Since the reactions of the supports and connections can be determined by considering the whole truss as one free body, the three unknown of the sectional part is usually forces in truss members. If the dimensions of truss members is known, only the magnitude of force in a truss member is the unknown.
Since the section is a virtual section only, there is no limitation of the shape of the sectional line or curve. The strategy of forces in truss member determination by method of sections is to start with maximum three unknowns. However, the method of sections in some case can be used to determine forces in the involved truss members that are more than three unknowns. If some of the unknown forces in truss members, which are connected by the joint pins, may be related and determined by setting up additional equilibrium equations through the construction of simple force vector diagram.
In order to maintain in static equilibrium state, after dividing the truss member into two sectional parts, there are alway reaction forces act on each other due to the forces in truss members. The force in the truss member can be assumed either tensile or compressive, the sense of the direction will confirm whether the assumption is correct or not. These two unknown forces becomes the external forces of the free body, sometimes these two unknown forces can directly act on the joint pin of the free body along the truss members because of the principle of transmissibility. Either of two sectional parts of the truss can be used as a free body for determining the forces in the truss members.

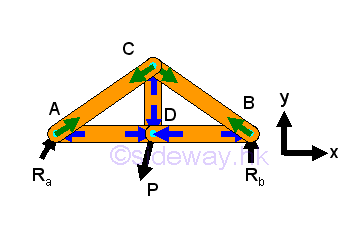
Determination of Forces in Trusses :
When the completely constrained truss is in static equilibrium, all the unknown reactions can be determined as in method of joints. Imply
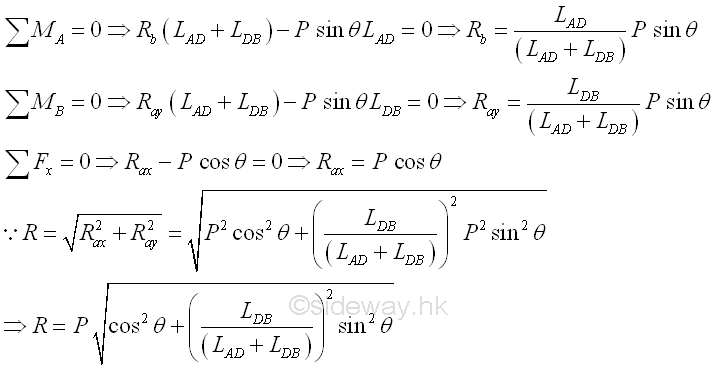
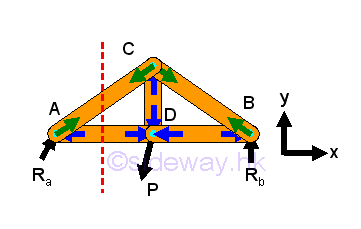
Forces in Two Truss Members AD and AC:
The left sectional part of the truss is a free body with two unknowns only, the forces in truss members can be determined by method of joints. Since there is only one joint in the free body, the equilibrium equations used is same as the equilibrium equations used in the method of joints Imply,
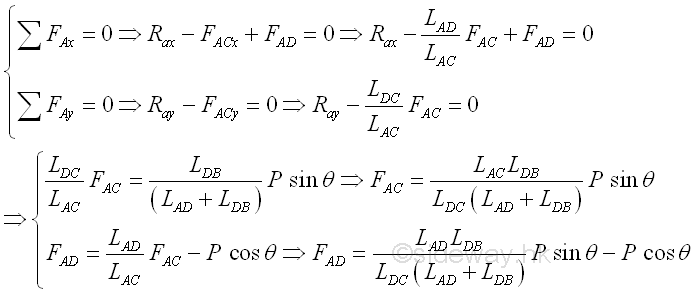
The right sectional part of the truss is a free body with two unknowns only, the forces in truss members can be determined by method of sections. For two unknowns, only two equilibrium equations are needed, Imply,
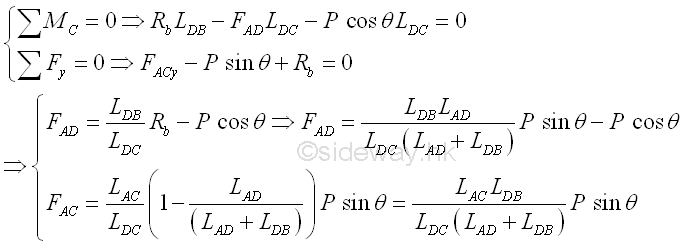
Forces in Three Truss Members AC, DC and CB:
The free bodys of the sectional parts is,

Considering the simple free body of the right sectional part of the truss with three unknowns and one reaction only. The forces in truss members can be determined by method of sections. For three unknowns, three equilibrium equations are needed. When the truss in equilibrium, the summation of moment at any point on the truss is equal to zero also. To simplify the analysis, forces truss can be obtained by taking moment at joints A, C and D, Imply
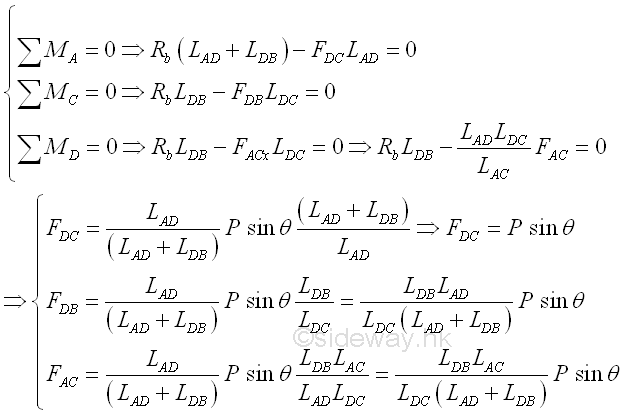
Forces in Four Truss Members AC, DC and CB:
This is only to demonstrate the creation of additional equilibrium equation for a four unknowns problem. ,
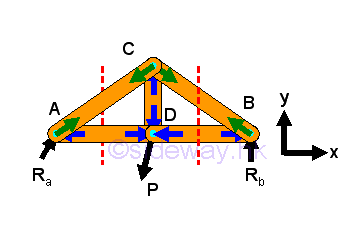
The free bodys of the sectional parts is,
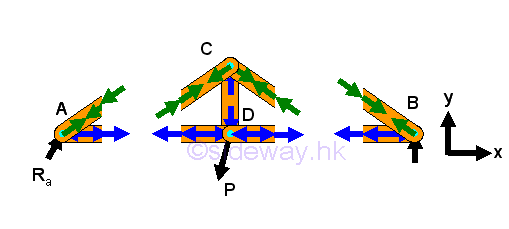
Considering the free body of the middle sectional part of the truss with four unknowns and one applied load only. The forces in truss members can also be determined by method of sections. For four unknowns, four equations are needed. Besides the three equilibrium equations, one more equation is need. According to the entire truss consturction, unknown forces either FDB and FCB, or FAD and FAC can related, Imply
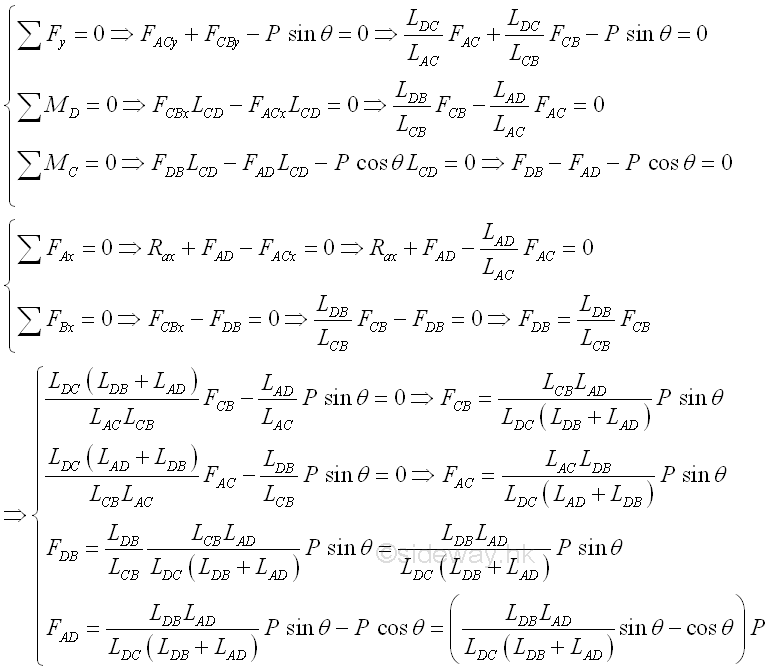
©sideway
ID: 120200074 Last Updated: 2/29/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 31
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
