Content
Transpose of a matrix
Transpose of a matrix,
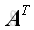 or
or
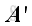
Properties of Matrix Transpose
Matrix Products Transpose
Transpose of Inverse Matrix
Transpose of a matrix
Transpose of a matrix,
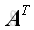 or
or
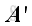
The transpose of a matrix, written as
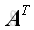 , is obtained by interchanging the rows and
columns of the original matrix
A.
Therefore if
, is obtained by interchanging the rows and
columns of the original matrix
A.
Therefore if
 amd
amd
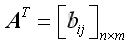 , the elemnt,
, the elemnt,
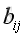 of matrix
of matrix
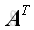 equals to the element,
equals to the element,
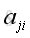 of matrix,
A.
And if the order of
A
is m x n then the order of
of matrix,
A.
And if the order of
A
is m x n then the order of
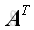 is n x
m.
is n x
m.
For example,
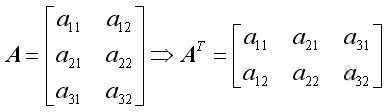
Properties of Matrix Transpose
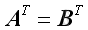 , if and only if
, if and only if
 .
.
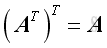
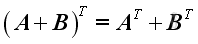
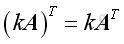
Matrix Products Transpose
if the matrix multiplication of
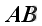 exists, then
exists, then
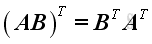 .
.
Since
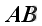 is defined,
is defined,
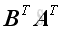 is also defined while
is also defined while
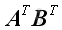 may not be.
may not be.
Let
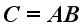 , where
A
is of order m x n and
B
is of order n x r, and
C
is of order m x r then
, where
A
is of order m x n and
B
is of order n x r, and
C
is of order m x r then
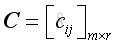 and element of
C is
and element of
C is
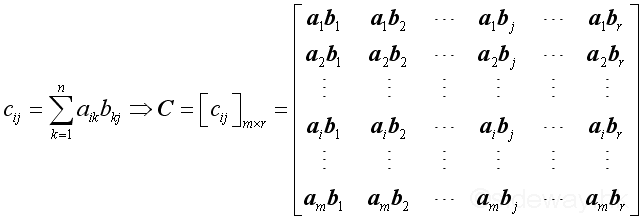
Let D is the transpose of C, then
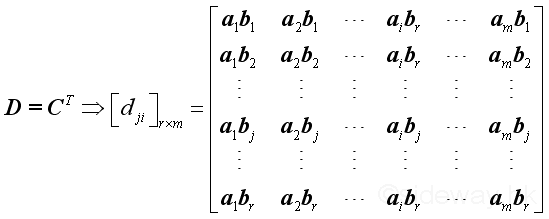
That is element in the row j and colume i of matrix D equals to product of row i of matrix A and column j of matrix B, that is
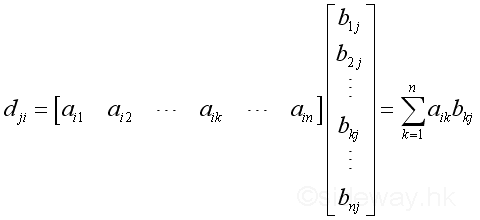
Let
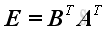 , since
, since
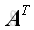 is of order n x
m and
is of order n x
m and
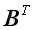 is of order r x
n, then
E
is of order r x m.
is of order r x
n, then
E
is of order r x m.
Let X be the transpose of A, imply
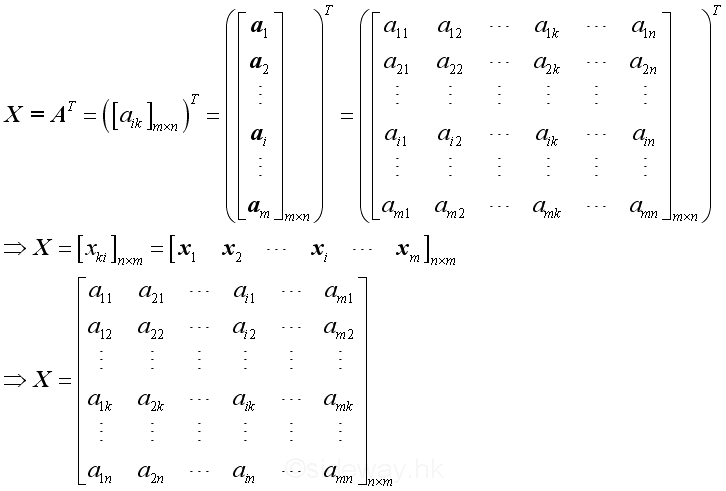 ,
,
Let Y be the transpose of B, imply
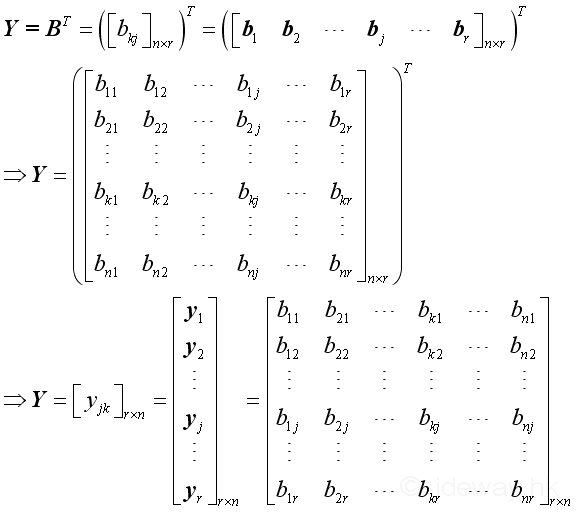
and imply
 ,
,
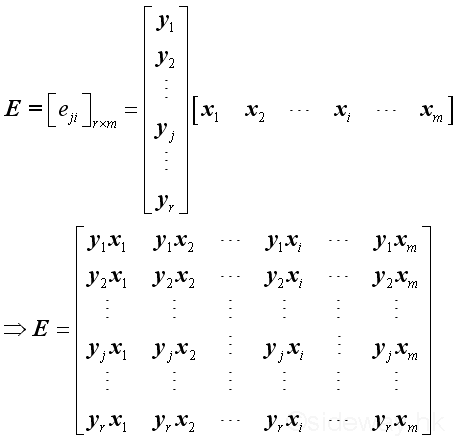
That is element in the row j and colume i of matrix E equals to
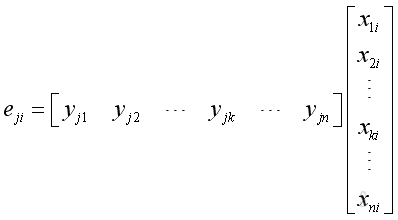 ,
,
Subsitute corresponding elements in row of matrix B and in column of matrix A imply
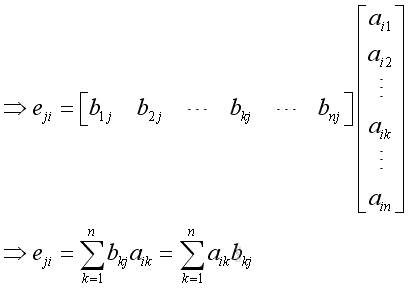 ,
,
And equals to the element of
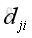 .
Therefore
.
Therefore
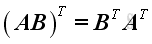
Transpose of Inverse Matrix
If
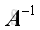 exists, then
exists, then
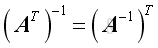 .
Since
.
Since
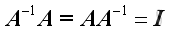 and
and
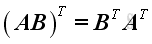 , imply
, imply
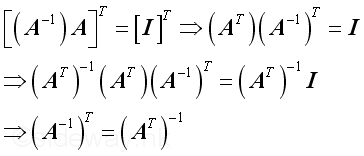 ,
,
©sideway
ID: 100800011 Last Updated: 8/14/2010 Revision: 0
Latest Updated Links
- Aqua-Pure Ap1610(last updated On 11/6/2025)
- Ikea PÅLYCKE clip-on hook rack(last updated On 11/5/2025)
- Ikea SANDSBERG table(last updated On 11/4/2025)
- Ikea TISKEN toilet roll holder(last updated On 11/3/2025)
- Philips CL400 Ceiling Light 36W(last updated On 11/2/2025)
- Philips CL400 Ceiling Light 24W(last updated On 11/1/2025)
- Philips CL400 Ceiling Light 13W(last updated On 10/30/2025)
- Ikea TISKEN basket(last updated On 10/29/2025)
- Ikea TISKEN towel rack(last updated On 10/28/2025)
- Ikea REXBEGONIA mattress protector(last updated On 10/27/2025)
- Ikea KEJSAROLVON mattress protector(last updated On 10/26/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 29![]()
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
