General Vector Space

A vector space is also called linear vector space and is the name used to describle a collection of objects called vectors. In other words, a vector space can be considered as a set and vectors are elements of the set. Euclidean vector space are the most common vector space for representing physical quantities which are usually visualized in form of an arrow-like vector. However, for vectors in 𝑛-space, the form of vectors do not necessarily to be an arrow-like object. Besides, the form of element is also not limit to numeric numbers.

Notations and Conventions

Let set 𝑆 or other capital letter be an 𝑛-tuple vector space or 𝑛-space. Elements of set 𝑆, 𝑛-tuples, are usually represented by a bold face capital letter, e.g. 𝑨=(𝐴₁,𝐴₂,⋯,𝐴_𝑛), and elements of the 𝑛-tuple 𝑨, i.e. (𝐴₁,𝐴₂,⋯,𝐴_𝑛) are called components of 𝑨. And for convenient, components of 𝑨 can be expressed as indexed elements with corresponding capital letter, i.e. 𝐴_𝑖, where 𝑖=1,2,⋯,𝑛. An ordered 𝑛-tuple vector is always the element of an 𝑛-tuple space.

Real Vector Space

Real vector space is one of the common vector space, for example ℝ², ℝ³ for 2-, 3-dimensional space. A vector space is named real vector space because components of all vector elements in the real vector space are real numbers. A real vector space itself is a collection of vector objects on which two standard operations, namely addition and scalar multipication, with typical properties are defined. In other words, a collecton of vector objects is called a real vector space only if the defined addition and scalar multiplication operations for all given vector objects satisfy all typical properties of addition and scalar multiplication operations for a real vector space.

Addition and Scalar Multiplication Operations

The addition and scalar multiplication operations is a rule set used to govern the available operations for real vector space.

• Addition Operation is a rule for associating a vector object with another two vector objects in a real vector space through the binary addition operation of two vector objects in specified order. For example, let 𝑛=3. Let 𝒂=(𝐴1,𝐴2,𝐴3); 𝒃=(𝐵1,𝐵2,𝐵3); 𝒂,𝒃∊ℝ3 Addition Operation: 𝒂+𝒃→𝒄 ⇒𝒂+𝒃=(𝐴1,𝐴2,𝐴3)+(𝐵1,𝐵2,𝐵3)=(𝐴1+𝐵1,𝐴2+𝐵2,𝐴3+𝐵3)=𝒄. ∎
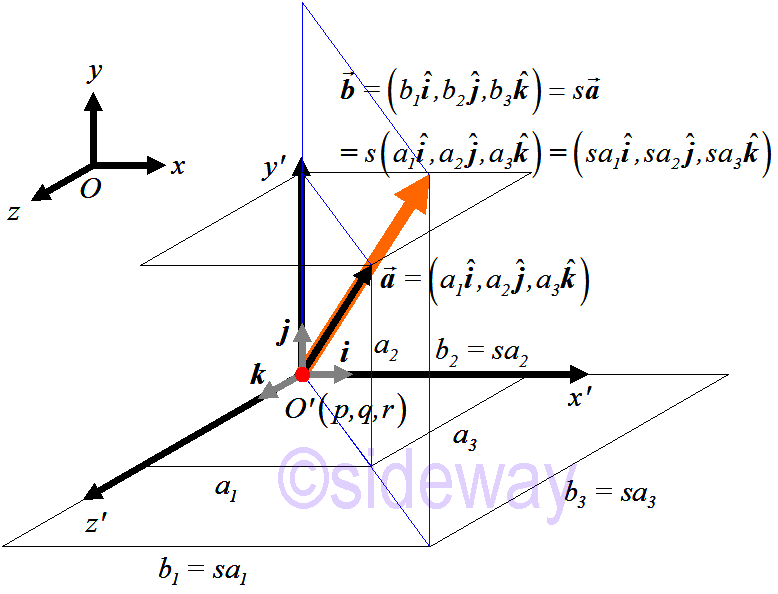
• Scalar Multiplication Operation, or called multiplication by a real number operation, is a rule for associating a vector object with another vector object in a real vector space through the binary scalar multiplication operation of a real number and the given vector object in the specified order. For example, let 𝑛=3. Let 𝒂=(𝐴1,𝐴2,𝐴3); 𝒂∊ℝ3; 𝑠∊ℝ Scalar Multiplication Operation: 𝑠𝒂→𝒃 ⇒𝑠𝒂=𝑠(𝐴1,𝐴2,𝐴3)=(𝑠𝐴1,𝑠𝐴2,𝑠𝐴3)=𝒃. ∎

Definition of Real Vector Space

Real Vector SpaceLet the elements of set 𝑆 be ordered 𝑛-tuple vectors of real numbers. Let 𝑨 be (𝐴1,𝐴2,⋯,𝐴𝑛), 𝑩 be (𝐵1,𝐵2,⋯,𝐵𝑛) where 𝐴𝑖 and 𝐵𝑖 are real numbers and 𝑖=1,2,⋯,𝑛. If elements of set 𝑆 satisfy the following operation properties: Addition Property: 𝑨+𝑩=(𝐴1,𝐴2,⋯,𝐴𝑛)+(𝐵1,𝐵2,⋯,𝐵𝑛)=(𝐴1+𝐵1,𝐴2+𝐵2,⋯,𝐵𝑛+𝐵𝑛) Scalar Multiplication Property: 𝛽𝑨=𝛽(𝐴1,𝐴2,⋯,𝐴𝑛)=(𝛽𝐴1,𝛽𝐴2,⋯,𝛽𝐴𝑛), where 𝛽 is any real number Then set 𝑆 is called Real Vector Space.

Algebraic Properties

The addition and scale multiplication properties is only used to define the available operations for a real vector space. Two fundamental properties of vector elements are needed to be defined before defining the specific properties of binary operations of real vector space. The equal and zero properties are used to clarify the basic algebraic properties of vector elements in real vector space.

• Equal Property is used to specify the equality of two vector objects and two vector objects are equivalent only if all corresponding components of two vector objects are equal. That is Let 𝒂=(𝐴1,𝐴2,⋯,𝐴𝑛); 𝒃=(𝐵1,𝐵2,⋯,𝐵𝑛) Equal Property: 𝒂=𝒃 ⇒(𝐴1,𝐴2,⋯,𝐴𝑛)=(𝐵1,𝐵2,⋯,𝐵𝑛) ∵ two vector elements are equivalent only if every corresponding components of two vector elements have the same value, and vice versa. ⇒𝐴𝑖=𝐵𝑖, where 𝑖=1,2,⋯,𝑛. ∎
• Zero Property is used to specify the zero property of a zero vector object, denoted by 𝟎, and a vector named zero vector only if all components of the vector are equal to zero. That is Let 𝒂=(𝐴1,𝐴2,⋯,𝐴𝑛); zero vector: 𝟎=(0,0,⋯,0) Zero Property: 𝒂=𝟎 ⇒(𝐴1,𝐴2,⋯,𝐴𝑛)=(0,0,⋯,0) ∵ Equal Property: two vector elements are equivalent only if every corresponding components of two vector elements have the same value, and vice versa. ⇒𝐴𝑖=0, where 𝑖=1,2,⋯,𝑛. ∎

Definition of Algebraic Properties

Algebraic PropertiesThe two fundamental algebraic properties of 𝑛-tuples in real vector space are: Equal Property : Two 𝑛-tuples 𝑨 and 𝑩 are equal if and only if 𝑨𝑖=𝑩𝑖, where 𝑖=1,2,⋯,𝑛. Zero Property : A 𝑛-tuple is called zero 𝑛-tuple if and if only all components of the 𝑛-tuple are equal to 0, that is (0,0,⋯,0). A zero 𝑛-tuple is denoted by 𝟎.