Content
General Equations of Kinematics
Equations of 1D Kinematics
Acceleration as a function of time t
Acceleration as a function of position
Acceleration as a function of velocity
General Equations of 1D Kinematics
General Equations of Kinematics
From the instantaneous situation, similar equations of 1D kinematics can be used to calculate the unknown quantity from the known quantities for 1D motion.
Equations of 1D Kinematics
Acceleration as a function of time t
The motion of an object is described with respect to time. From the Instantaneous Situations, general equations of 1D kinematics are derived to calculate unknown quantity for the motion of an object as following.
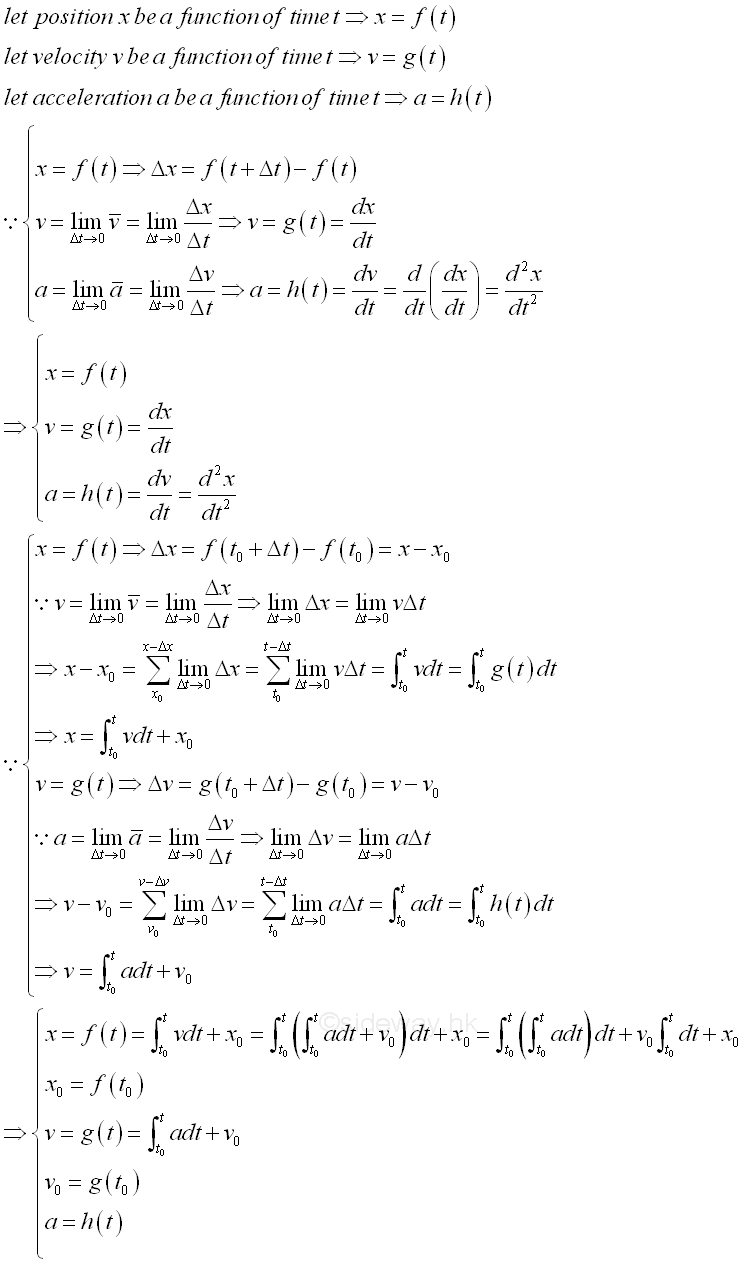
For uniform motion where a=0, imply.
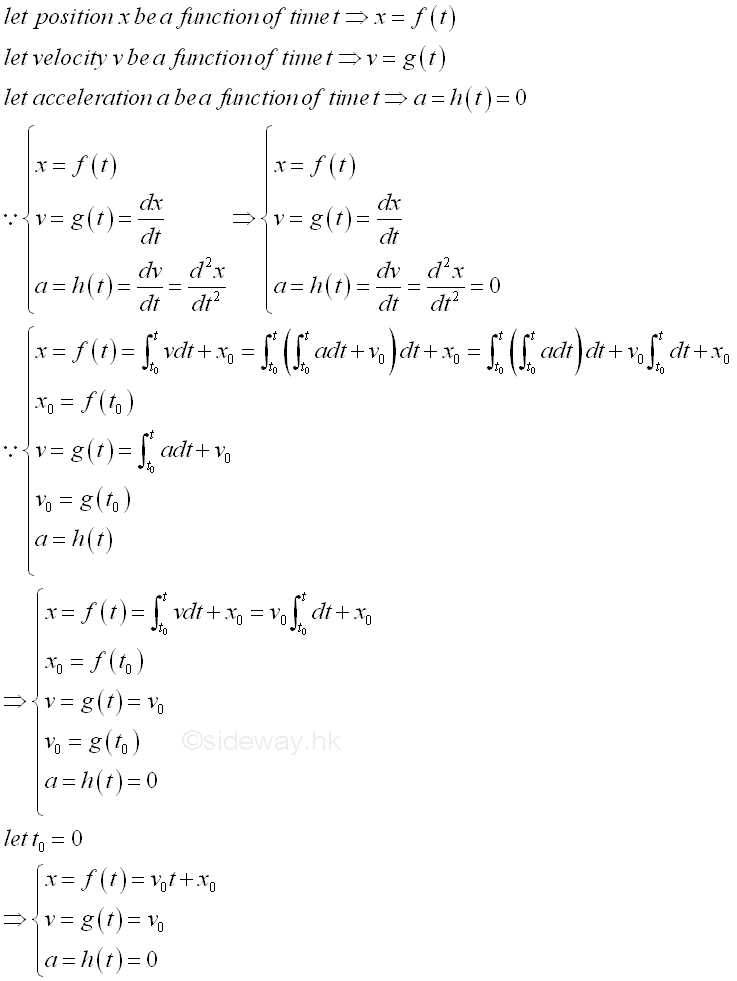
For uniformly accelerated motion where a=constant, imply.
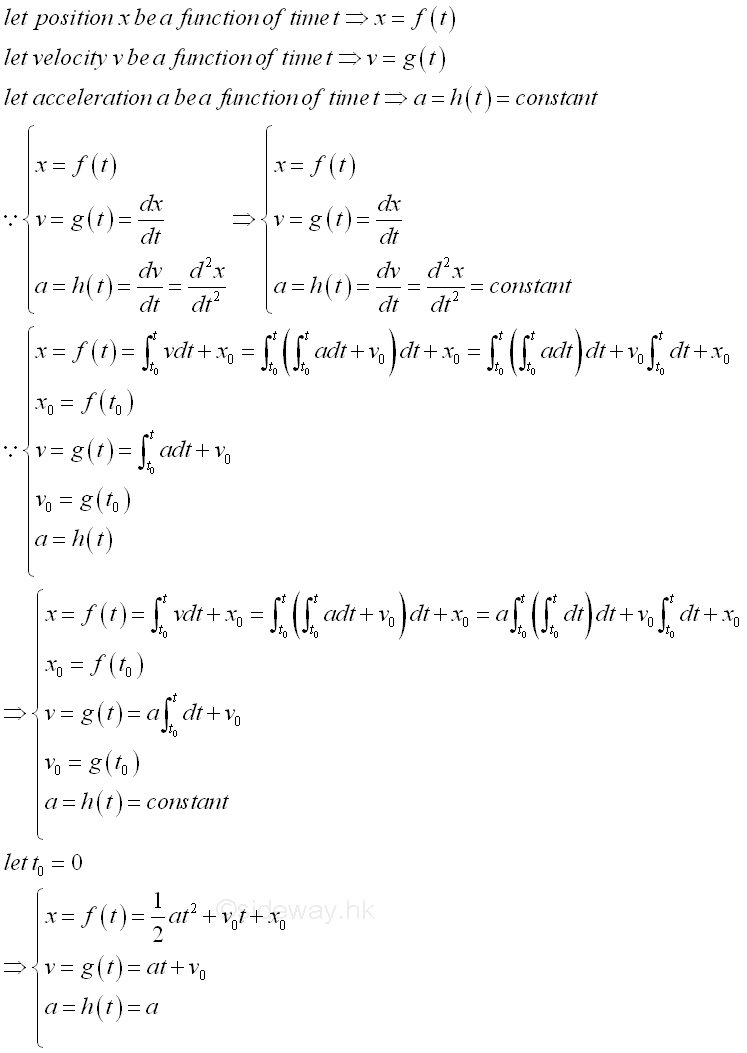
Acceleration as a function of position
When position is a function of time, the motion of an object can also be described with respect to position, if time t can also be expressed as a continuous function of position x. From the instantaneous situations, both the instantaneous velocity and instantaneous acceleration with respect to the time t are also related to same position x as position x is a function of time t.

For uniform motion where a=0, imply.
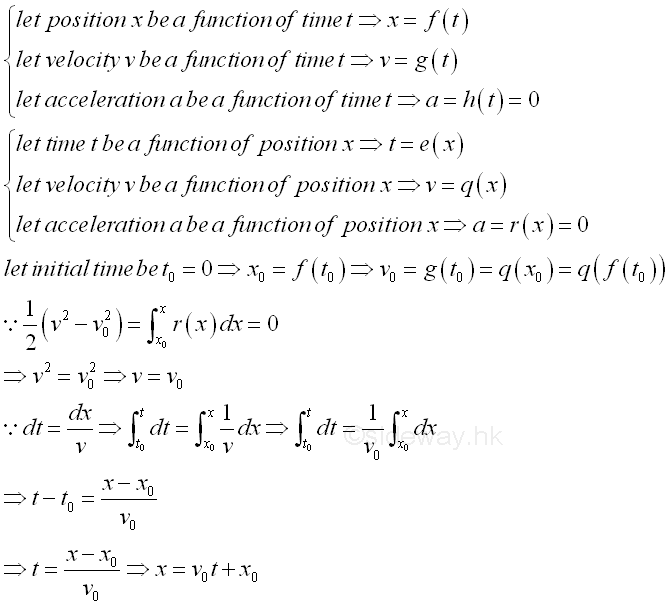
For uniformly accelerated motion where a=constant, imply.

Acceleration as a function of velocity
When velocity is a function of time, the motion of an object can also be described with respect to velocity, if time t can also be expressed as a continuous function of velocity v. From the instantaneous situations, both the position and instantaneous acceleration with respect to the time t are also related to same velocity v as velocity x is a function of time t.

For uniform motion where a=0, imply.

For uniformly accelerated motion where a=constant, imply.

General Equations of 1D Kinematics
General equations of 1D kinematics are.

©sideway
ID: 140200014 Last Updated: 2/14/2014 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Pentium(last updated On 7/3/2025)
- Intel CPU(last updated On 7/2/2025)
- Intel CPU History(last updated On 7/1/2025)
- FreeGLUT Windows Function(last updated On 1/27/2025)
- FreeGLUT Initialization Function(last updated On 1/26/2025)
- FreeGLUT(last updated On 1/25/2025)
- GLUT(last updated On 1/24/2025)
- OpenGL(last updated On 1/23/2025)
- XPower UC140 4-Port 140W PD3.1 GaN Travel Charger(last updated On 1/22/2025)
- XPower DX6 6 In 1 (2x3) 60W PD3.0 Sync & Charge Cable(last updated On 1/21/2025)
- XPower MF240 1.2M Magnetic Absorption 4 in 1 (2x2) Zinc Alloy 240W PD Sync & Charge Cable(last updated On 1/20/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Computer
Hardware 257
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
