Content
Relative Motion
Relative Independent Motion of Two Objects
Relative dependent Motion of Objects
Relative dependent Motion of Two Objects
Relative dependent Motion of
Serveral Objects
Relative Motion
In practical engineering problems, several objects moving along a line can also be related to each other. Usually, the system of objects are measured by a single time system with the same measurement dimension.
Relative Independent Motion of Two Objects
Sometime the observation of the motion of an object is not carried out on a static object. In other word, the place to measure the motion of another is on a moving object also. The result of the observed motion is difference from the observation observed on a static object with a static origin point.
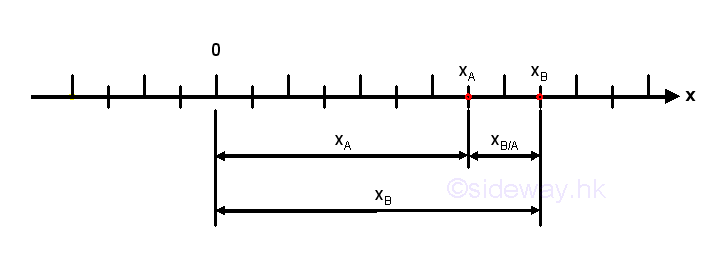
When an object A is located on a straight line, the position xA of the object is referenced to the origin O. If another independent object B is located on the same straight line with the same reference O, where the position xB of the object is also referenced to the origin O, then the difference xB-xA is called the relative position coordinate of B with respect to A, that is xB/A. Since xA is used as the reference point of xB when measuring the relative position coordinate xB/A , a positive sign means that position B is to the right of position A while a negative sign means that position B is to the left of position A and the sign is regardless of the positions of A and B with respect to the static origin O.
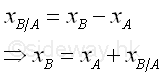
When both objects A and B are moving on the same straight line, both the rates of change of position with respect to time t, vA and vB , at positions xA and xB accordingly are referenced to the static origin O.
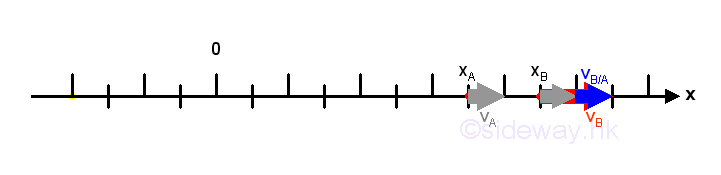
The difference vB-vA is called the relative velocity of object B with respect to object A, that is vB/A. Since object A is used as the reference object of object B, when measuring the relative velocity vB/A, the rate of change of position of object A, vA is remove from the rate of change of position of object B, vB. In other words, the relative velocity of object B with respect to object A is observed from object A instead of rom the static origin O. Therefore, a positive sign means that object B moves in the positive direction when observing from object A while a negative sign means that object B moves in the negative direction when objeserving from object A, and the sign is regardless of the absolute velocity of A and B with respect to the static origin O.
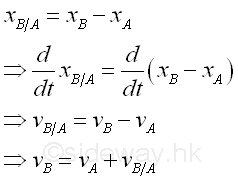
Similarly, when both objects A and B are accelerated on the same straight line, both the rates of change of velocity with respect to time t, aA and aB , at positions xA and xB accordingly are referenced to the static origin O.
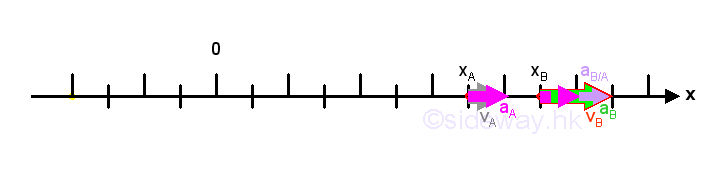
The difference aB-aA is called the relative acceleration of object B with respect to object A, that is aB/A. Since object A is used as the reference object of object B, when measuring the relative acceleration aB/A, the rate of change of velocity of object A, aA is remove from the rate of change of velocity of object B, aB. In other words, the relative acceleration of object B with respect to object A is observed from object A instead of rom the static origin O. Therefore, a positive sign means that object B accelerates in the positive direction when observing from object A while a negative sign means that object B accelerates in the negative direction when objeserving from object A, and the sign is regardless of the absolute acceleration of A and B with respect to the static origin O.
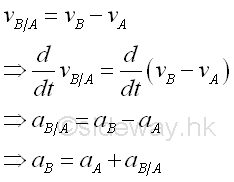
Relative dependent Motion of Objects
Besides independent motion, sometime the motion of an object is depended on the motion of other objects. When objects are linked together, the position of an object is depended on the positions of other linked object. And therefore the relative motion of objects are dependent on each others.
Relative dependent Motion of Two Objects
For example, when object A at xA moves distance GxA up, then object B at xB will move distance GxB down. And GxB equals GxA since the total cable length is a constant, The sum of xA and xB is always equal to a constant since (xA-ΔxA)+(xB+ΔxB)=(xA-ΔxA)+(xB+ΔxA) is always equal to a constant regardless of the positions of xA and xB.
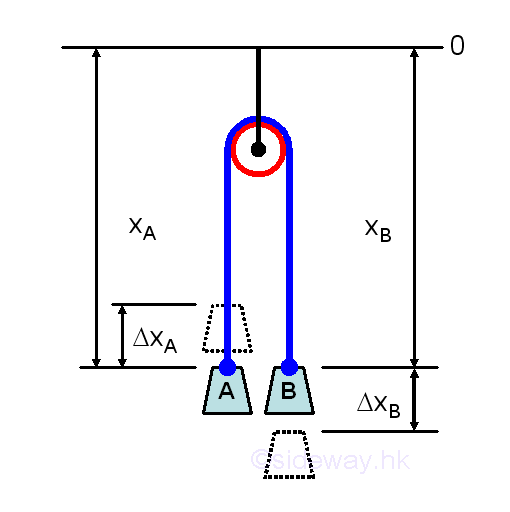
That is.

For another example, when object A at xA moves distance GxA up, then object B at xB will move distance GxB down. And 2GxB equals GxA since the total cable length is a constant, The sum of xA and 2xB is always equal to a constant since (xA-ΔxA)+2(xB+ΔxB)=(xA-ΔxA)+2(xB+ΔxA/2) is always equal to a constant regardless of the positions of xA and xB. As xA+2xB =constant, the system is fixed once one of the position of the two objects A and B is defined and therefore the system has one degree of freedom only.
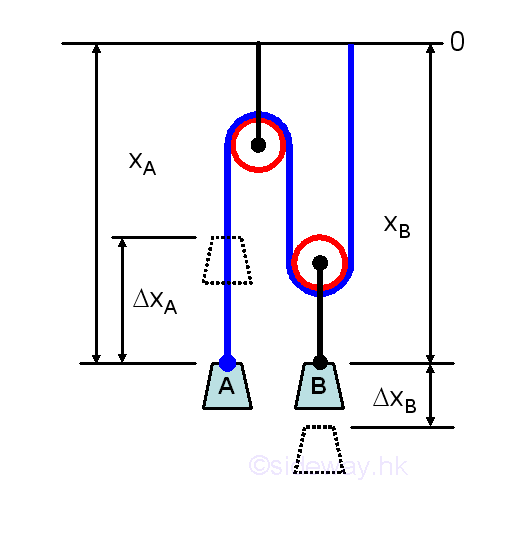
That is.
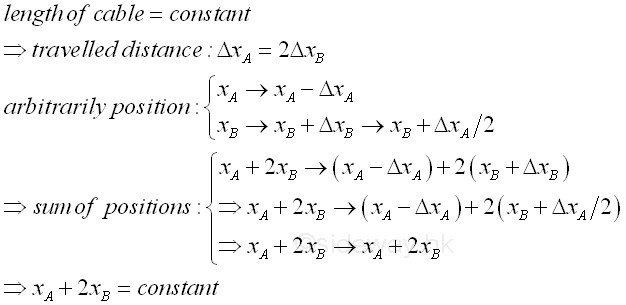
Relative dependent Motion of Serveral Objects
If one more object C is added to the system, when object A at xA moves distance GxA up, then the motions of objects B and C are not known until one of the motions of object B or object C is fixed. let object B at xB moves distance GxB down. and object C at xC moves distance GxC down. Then GxA=2GxB+2GxC since the total cable length is a constant. Therefore the sum of xA , 2xB , and 2xC is always equal to a constant since (xA-GxA)+2(xB+GxB)+2(xC+GxC)=(xA+2GxB+2GxC)+2(xB-GxB)+2(xC-GxC) is always equal to a constant regardless of the positions of xA, xB and xC. As xA+2xB+2xC =constant, the system is fixed only when two of the position of the three objects A, B and C is defined and therefore the system has two degrees of freedom.

That is.

Since the relative dependent motions between particles are linear, a simple relationship between the velocity or acceleration of objects can be obtained, that is the rate of change is also linear with respect to time. Both the velocity and acceleration of objects can be obtained by differentiation. Imply
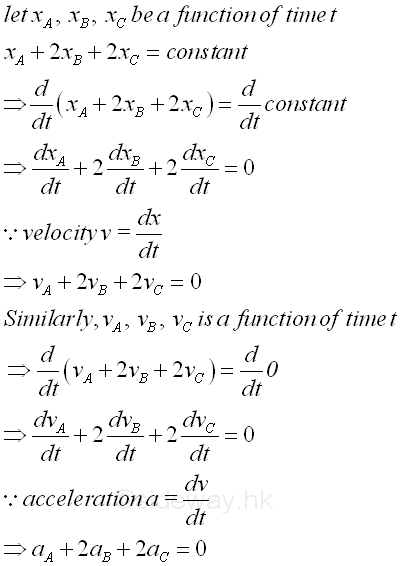
©sideway
ID: 140200016 Last Updated: 3/6/2014 Revision: 1 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Pentium(last updated On 7/3/2025)
- Intel CPU(last updated On 7/2/2025)
- Intel CPU History(last updated On 7/1/2025)
- FreeGLUT Windows Function(last updated On 1/27/2025)
- FreeGLUT Initialization Function(last updated On 1/26/2025)
- FreeGLUT(last updated On 1/25/2025)
- GLUT(last updated On 1/24/2025)
- OpenGL(last updated On 1/23/2025)
- XPower UC140 4-Port 140W PD3.1 GaN Travel Charger(last updated On 1/22/2025)
- XPower DX6 6 In 1 (2x3) 60W PD3.0 Sync & Charge Cable(last updated On 1/21/2025)
- XPower MF240 1.2M Magnetic Absorption 4 in 1 (2x2) Zinc Alloy 240W PD Sync & Charge Cable(last updated On 1/20/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Computer
Hardware 257
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
