Content
Rules of Integration for Indefinite
Integral
Method of Partial Fractions for
Indefinite Integral
Integration by Partial Fractions
Rules of Integration for Indefinite Integral
Method of Partial Fractions for Indefinite Integral

where Φ(x) and φ(x) are rational, integral, algebraical functions of x
The integrand after denominator factorization is

Integration by Partial Fractions
The method of integration by partial fractions can be expressed as

The integral of polynomial Q(x) can be obtained by making use of the constant multiple, sum of function properties of intergration and applying the anti-differentiation of the derivative of polynomial. The integration of the four case of fraction factors after partial fractions are:
-
linear partial fraction A/(ax+b)
This is the most common type of partial fraction, the integral of the linear partial fraction can be obtained by the quotient of standard functions rule of indefinite integral,

Therefore the integral of linear partial fraction can be determined by:
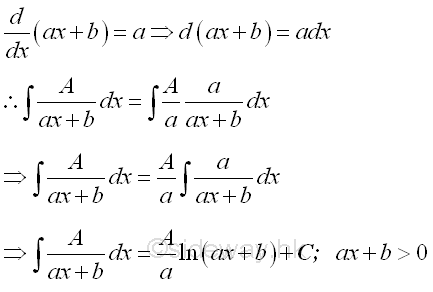
-
repeated linear partial fraction A/(ax+b)k
This is the most simple type of partial fraction.The integral of the repeated linear partial fraction can be obtained by product of standard functions rule of indefinite integral.

Therefore the integral of repeated linear partial fraction can be determined by:
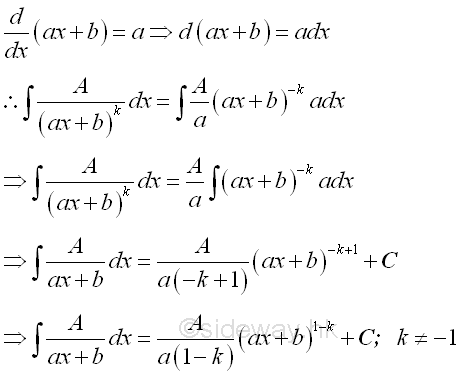
-
quadratic partial fractionr (Ax+B)/(ax2+bx+c)
For the quadratic partial fraction, there are some variant forms.
-
Standard quadratic partial fraction (Ax+B)/(ax2+bx+c).
-
If the numerator can be expressed as the derivative of the denumerator, imply
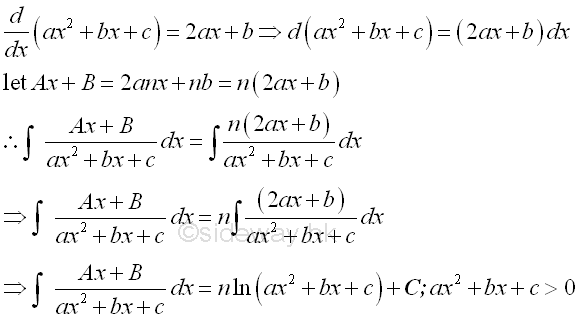
-
If the numerator can not be expressed as the derivative of the denumerator, imply

For the last integral, the quadratic factor can be resolved by completing the square, imply

Since the quadratic factor is irreducible, 4ac-b2>0, imply

Therefore the integral is

-
-
Quadratic partial fraction Ax/(ax2+bx+c). Same as a.ii case where B=0, imply

Quadratic partial fraction B/(ax2+bx+c). Same as the last integral in a.ii case where B=D, imply

- Quadratic partial fraction with quadratic factor, (ax2+bx)
Quadratic factor (ax2+bx) is same as (ax2+bx+c) by letting c=0, the integral can be obtained as in case a
- Quadratic partial fraction with quadratic factor, (ax2+c)
Quadratic factor (ax2+c) is same as (ax2+bx+c) by letting b=0, the integral can be obtained as in case a. But no complete the square is needed since the factor can be directly transformed into needed format., imply
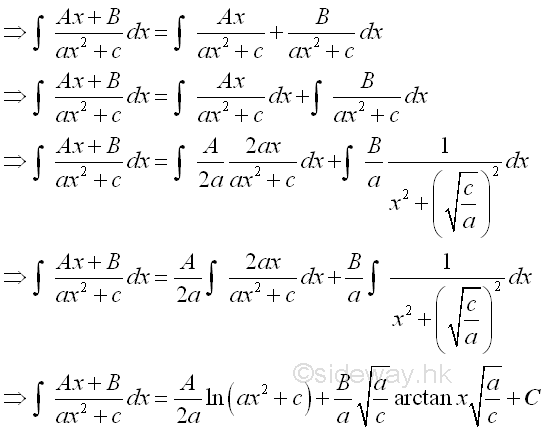
-
-
repeated quadratic factor (Ax+B)/(ax2+bx+c)k
The proceduce of determine the integral is same as case 3 except for the determining of the integral with power after decomposing the original integral into two integrals. Imply

The first integral can be obtained by simple substitution. Imply

The second integral can be obtained by simple substitution. Imply
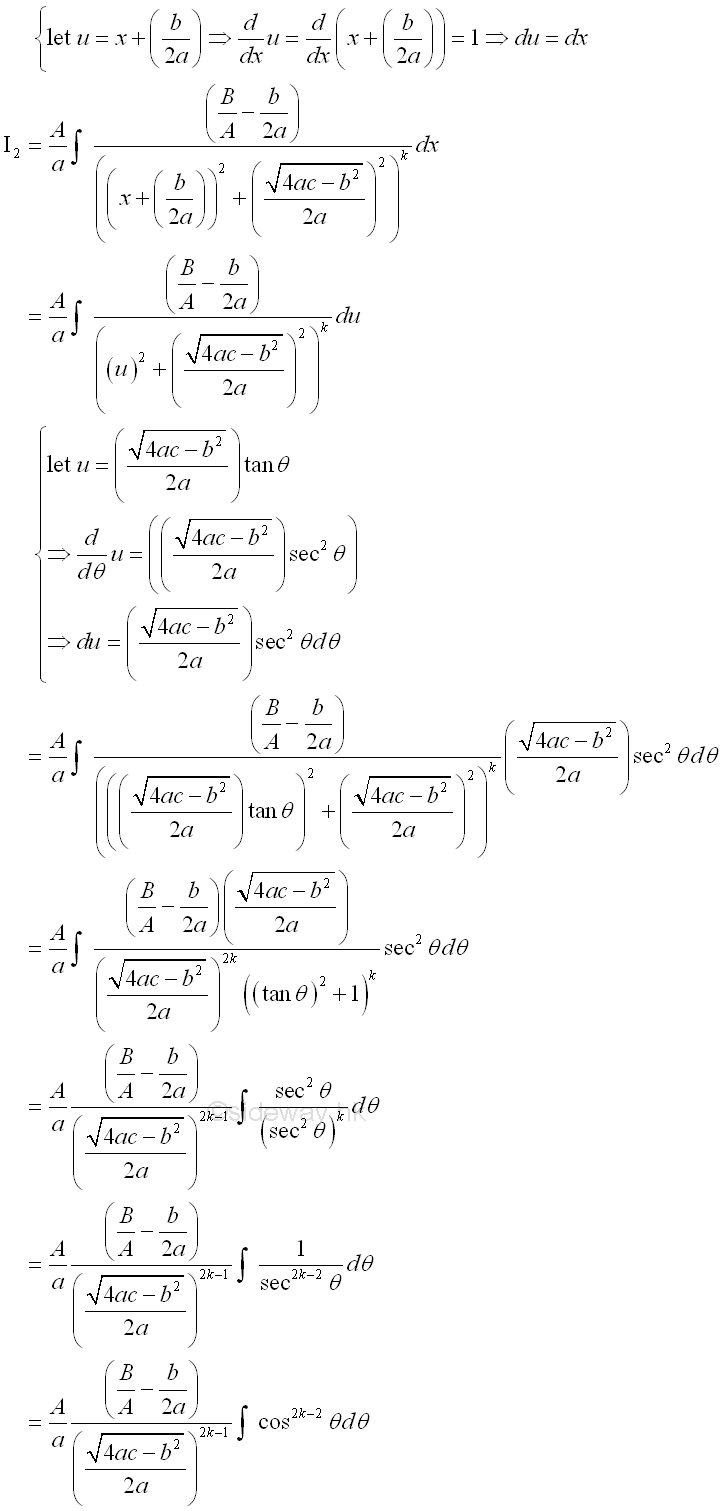
The second integral can further be expanded using the formule in integration by part as:
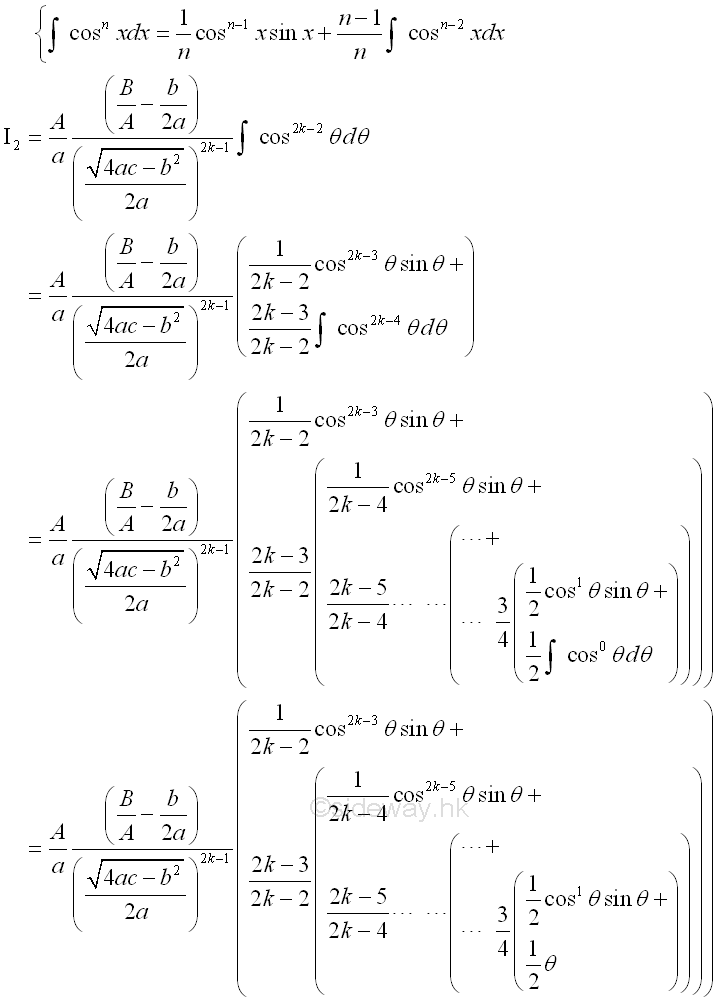
The theta angle can be transformed back to x through trigonometry, imply:
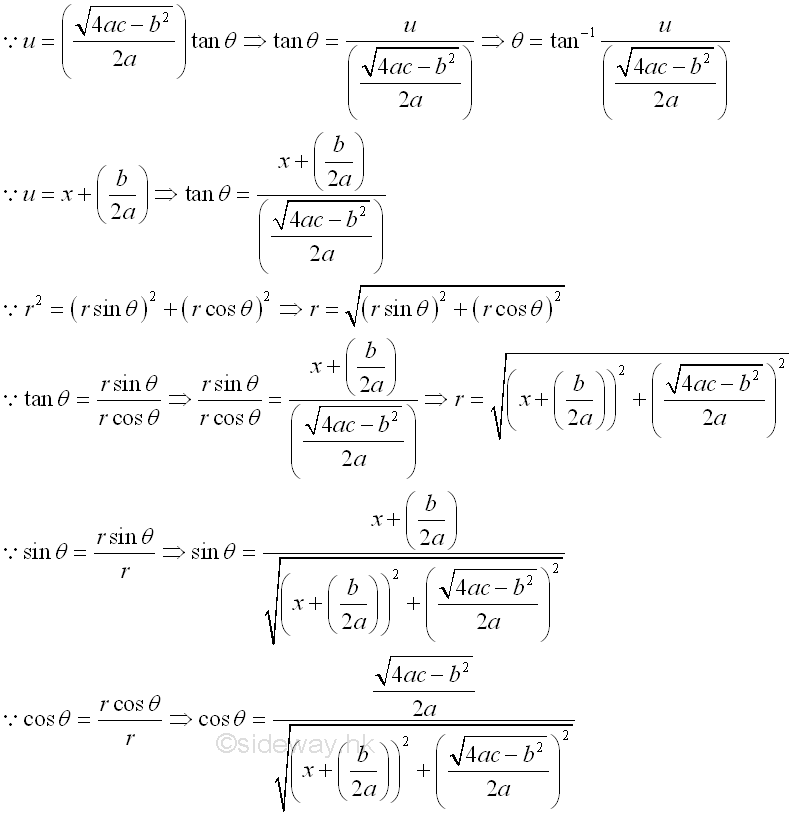
And the integral can be expressed as:


©sideway
ID: 111000033 Last Updated: 10/30/2011 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 22
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
