Content
Rules of Integration for Indefinite
Integral
Method of Partial Fractions for
Indefinite Integral
Partial Fractions Expansion
Coefficients Determination:
Techniques of Computing Coefficients
Rules of Integration for Indefinite Integral
Method of Partial Fractions for Indefinite Integral

where Φ(x) and φ(x) are rational, integral, algebraical functions of x
The integrand after denominator factorization is

Partial Fractions Expansion
The expansion of partial fractions is the process of converting the factors in the denominator to a sum of terms in which the denominator is determined by the denominator factors and the numerator is undetermined. Before proceeding the expansion, like terms of the factored denominator should be grouped in power form. The grouped terms in the denominator can be classified into two catalogues, linear term and quadratic term. The expansion of factor in each catalogue is governed by two rules. And the rules are summerized as following:
-
For a linear term ax+b, the format of the partial fraction expansion is
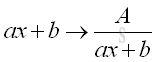
-
For a group of repeated linear term (ax+b)k, the pattern of the partial fractions expansion is

-
For a quadratic term ax2+bx+c, the format of the partial fraction expansion is
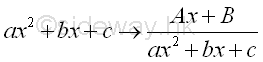
-
For a group of repeated quadratic term (ax2+bx+c)k, the pattern of the partial fractions expansion is
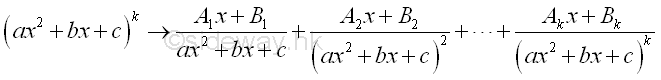
When letting k=1, the first and the third rules can be considered as the special case of the second and fourth rules respectively. In general, the factors in denominator can be rewritten as:
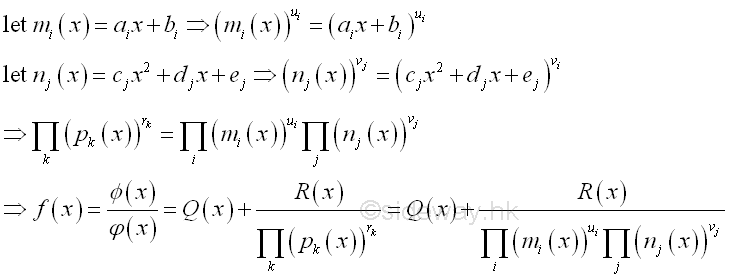
Therefore the integrand after partial fractions expansion is

Coefficients Determination:
After the factor expansion, a set of unknown coefficients A, C, D, are needed to be determined. These unknown coefficients can be calculated because the two sides of the equation. Therefore if the denominator on both sides of the equation are identical, the numerator on both sides of the equations are identical also. This can be achieved by ignoring the quotient function and considering the remaining rational function only.:
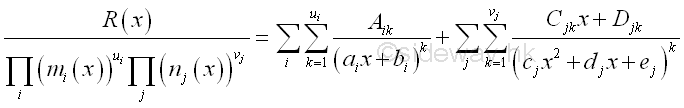
Since the denominator on the left side is the least common factor of the denominator on the right side, the equation of numerator can be obtained by cross-multiplying.
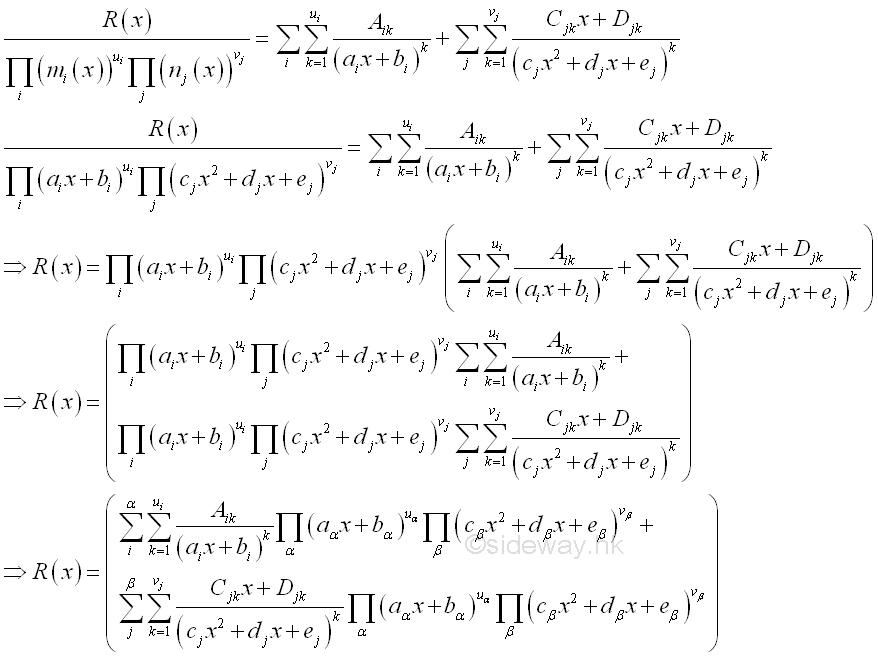
Therefore the coefficients can be determined by the equation of numerator. There are two methods to determine the coefficients:
-
Method of deducing coefficient
The strategy of this method is to make some terms of the numerator equation on the right side vanish by substituting convenient values.
Since all quadratic terms of partial fractions are irreducible, the deducing method is applied to the linear terms of partial fractions only. Imply coefficients can be deduced by substituting different values for x into the numerator equation.
Since roots of the original denominator can make the partial factor equal to zero, roots of the original denominator are the values of x for deducing coefficient. Imply
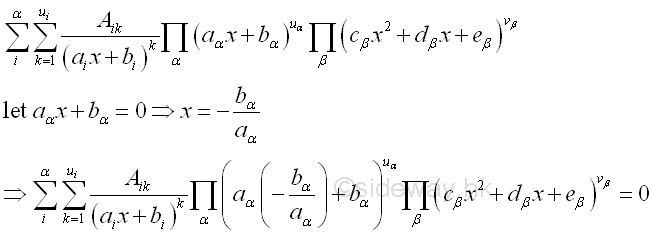
Besides, substiting suitable valves of x to the linear terms of quadratic factor can also make some quadratic factors on the right side of numerator equation equal to zero and vanish. Imply
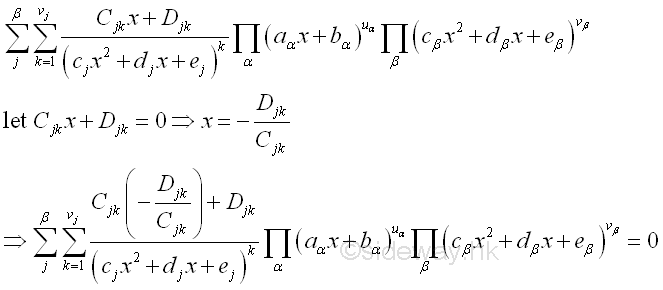
If the number of equation formed by direct substituting convenient value is less than the number of total undetermined coefficients. A simple value of x ,e.g. x=0, 1 can be used as the substiuting convenient value to create the necessary numbers of equations with minimum calculation work needed. imply

-
Method of comparing coefficients
The strategy of this method is to compare the coefficients on each degree of the polynomial on both sides of the numerator equation by expanding the numerator equation on the right side and grouping like terms together to determine the coefficients of each degree so that the coefficients on both sides can be compared degree by degree accordingly. Imply

If the number of equation formed by comparing coefficients is less than the number of total undetermined coefficients. A simple value of x ,e.g. x=0, 1 or convenient values can be used as the substiuting convenient value to create the necessary numbers of equations with minimum calculation work needed as in method of deducing coefficient.
Techniques of Computing Coefficients
In short, the method of deducing coefficient is the indirect generation of equation of coefficient through substiting convenient values to the numerator equation and the method of comparing coefficients is the direct generation of equation of coefficient through equating the coefficients on both sides of the numerator equation.
The strategy of applying these two techniques is similar to solving simultaneous linear equations of multiple variables. The simultaneous solutions set of the system of equation can be determined by using common algebrac techniques, e.g. method of elimination by substitution method, method of elimination by addition. The key differences beween them is the simulatneous linear equations is given while the system of coefficient equation is to be determined. The problem is to generate the useful equations for obtaining unit solution of the simultaneous linear equations.
The key step of solving simultaneous linear equations of multiple variables is to eliminate number of variable in equations to two, so that these two variables can nullify each other.
The method of deducing coefficients by substituting the root of original denominator can usually obtain simple coefficient equation. And the substition of convenient value 0 is same as determining the zero degree of the expanded equation, constant. Therefore for partial fractions with linear and repeated factors, the method of deducing coefficients is the most effective way to determine the unknown coefficients.
But for quadratic factors, the method of deducing coefficients using root of the original denominator alone does not always done the job. Sometime substiuting convenient value to create the necessary numbers of equations is needed in order to nullify the unknown coefficients. Method of comparing coefficients can usually acts as the complementary tool to complete system of equations by selecting the most suitable degrees of the coefficient equation for coefficient comparing. If there is no root of origninal denominator, the simultaneous equations for determining unknown coefficients can be set up by the method of comparing coefficients. The simultaneous solutions set of the system of equation can then be determined by using common algebrac techniques, e.g. method of elimination by substitution method, method of elimination by addition.
©sideway
ID: 111000027 Last Updated: 10/30/2011 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Precision Start Thermostat shower mixer(last updated On 11/8/2025)
- Tempesta 100 Shower Rail Set 3 sprays(last updated On 11/7/2025)
- Aqua-Pure Ap1610(last updated On 11/6/2025)
- Ikea PÅLYCKE clip-on hook rack(last updated On 11/5/2025)
- Ikea SANDSBERG table(last updated On 11/4/2025)
- Ikea TISKEN toilet roll holder(last updated On 11/3/2025)
- Philips CL400 Ceiling Light 36W(last updated On 11/2/2025)
- Philips CL400 Ceiling Light 24W(last updated On 11/1/2025)
- Philips CL400 Ceiling Light 13W(last updated On 10/30/2025)
- Ikea TISKEN basket(last updated On 10/29/2025)
- Ikea TISKEN towel rack(last updated On 10/28/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 31![]()
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
