Content

Kinetics: Conservation of Energy

Work done on an object by a force can change the dynamic property in term of kinetic energy. If the force acts upon the object is a conservative force, the work done can then be expressed in term of the potential energy with respect to the position of the object. Therefore, the change in kinetic energy due to the work done by a conservative force can be expressed in term of the change in pontential energy with respect to the position of the object. In other words, by neglecting other force acting on the an object, the sum of the pontential energy and kinetic energy of the object are conserved.

Conservative Forces

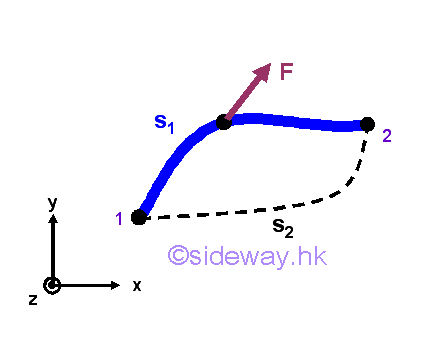
In a general sense, a force is conservative if the work done by the force acting on an object is independent of the path travelled by the object from the initial position to the final position, that is the work done by the force only depends on the initial and final position of the object. For examples, force of gravity, gravitational force and spring force.

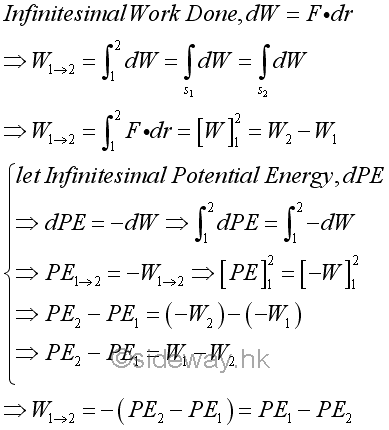
Therefore, the work done by an conservative force depends only on the pontential energy function with respect to the conservative force at the initial and final positions only. For a special case, if the final position coincides with the initial position, the potential energy at the initial and final position is equal and the work done by the force must be equal to zero.

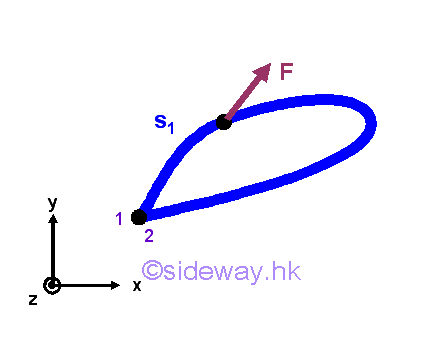
That is.

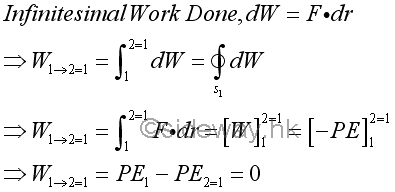
Scalar Function of a Conservative Force

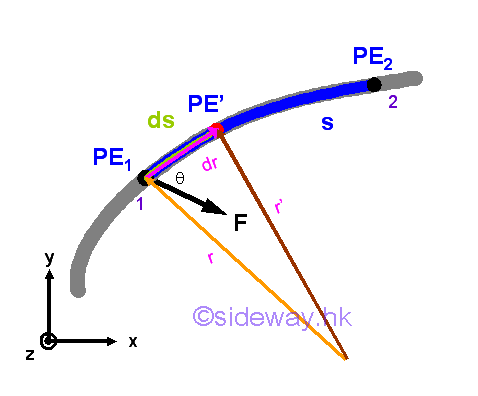
Since work done by a conservative force can be obained by either the product of force times displacement or the pontential energy function, a conservative force can derived from a potential energy function. That is

Since for any arbitrary potential energy function, the vector ∇×∇V is a zero vector, the vector ∇×F is a zero vector also. In other words, the line integral of work done by a conservative force is independent of the path followed by the object, when the infestimal work is an exact differential.

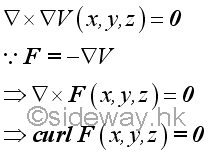
As a conservative force is derived from the gradient of a potential energy function, and the line integral around a closed path must be zero, the curl of a conservative force must be zero. And the curl of a force which is equal to zero is a necessary and a sufficient condition for a force to be conservative.

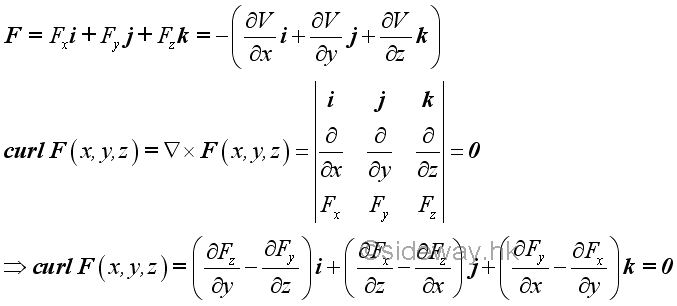
Conservation of Energy

Kinetically, the work done by a force on an object can be expressed in term of kinetic energy by the principle of work and energy.

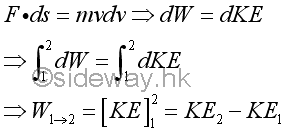
Physically, the work done by a conservative force on an object can be expressed in term of pontential energy with respect to the position of the object.

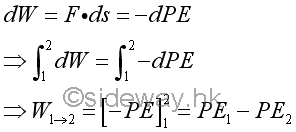
Therefore, the motion of an object caused by a conservative force can be described by equating the two forms of energy related to the work done by the conservative force. Since work done on an object by a conservative force decreases the potential energy and increases the kinetic energy or vice versa of the same magnitude, the sum of pontential energy and kinetic energy, which can be considered as the total mechanical energy of the capacity of the object related to the motion of an object, must remain constant during the motion.

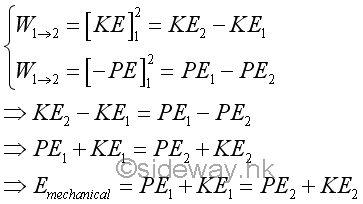
Mechanical Energy of a Pendulum

For example, a pendulum consists a bob of weight mg suspended by a weightless string of length r at a height of h above the ground. When the pendulum is released at position 1 with initial velocity v1, and the bob swings through a lower position 2, at which the instantaneous velocity is equal to v2, work is done by forces acting on the bob, and boht the kinetic energy and potential energy of the bob is changed accordingly also. Since the instantaneous velocity of the bob is always equal to the tangential velocity of the bob which is also equal to the speed of the bob.

The potential energies of the bob at position 1 and 2 are

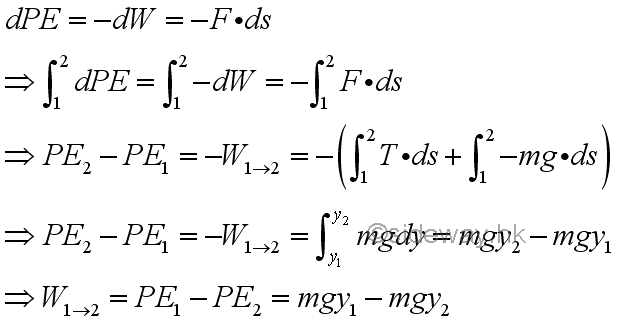
The kinetic energies of the bob at position 1 and 2 are

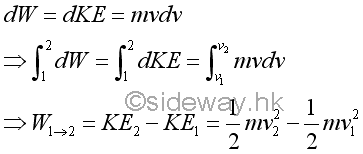
Therefore

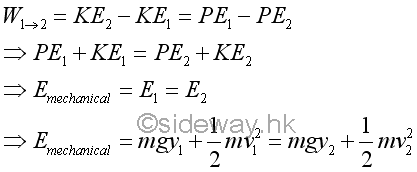
Since the kinetic energy difference of the bob is equal to the potential energy difference of the bob, the velocity of the bob can be expressed in terms of the potential energy of the bob. For example, if initial velocity v1 is equal to zero, the total mechanical energy in terms of potential energy is equal to

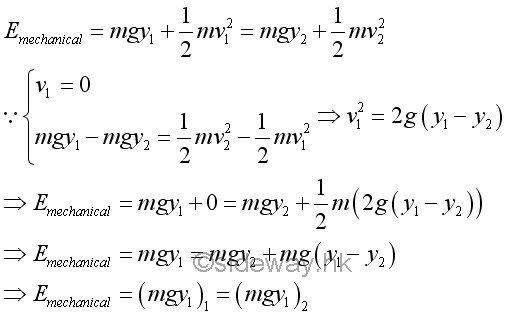
In other words, the magnitude of the instantaneous velocity or speed of the bob at any position can be determined using the principle of conservation of energy through the total mechanical energy of the bob. For example, the speed of the bob at position 3 is

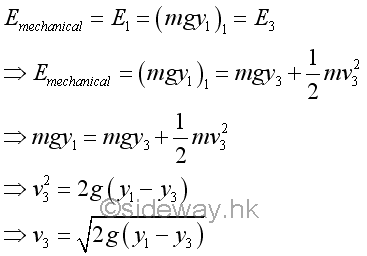
When the bob is released from position 1 to position 2 through position 3, the potential energy of the bob is decreased while the kinetic energy is increased. At position 1, the potential energy of the bob is maximum and the kinetic energy of the bob is equal to zero. At position 2, the potential energy of the bob is minimum and the kinetic energy of the bob is maximum. Since the kinetic energy of bob at position 2 is not equal to zero, the velocity of the bob is not equal to zero also. That is, the bob continues the motion and move to position 4 and position 5. At position 5, the kinetice energy of the bob becomes zero and the potential energy becomes maximum again. If the motion of the bob is not stopped at position 5, the force of gravity will cause the bob to fall down from position 5 to continue the motion of pendulum. 

Motion under Force of Gravity

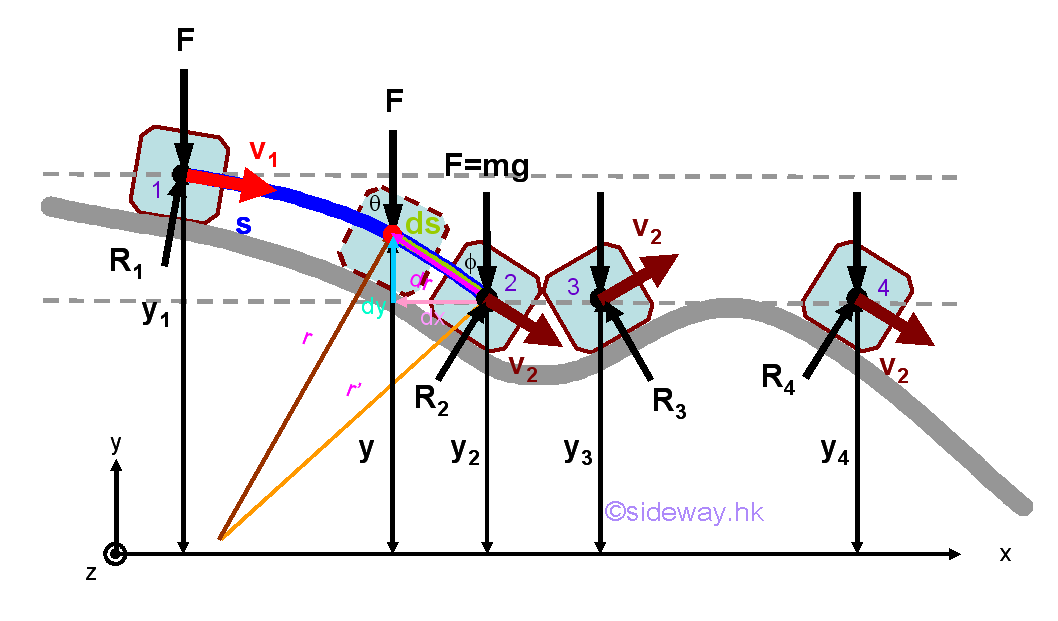
For an object slides down on a smooth track where friction force can be neglected, the reaction force act on the object by the track is always normal to the track along the path of motion. Similarly, the normal reaction force does no work and work is done only by force of gravity acting on the object, the principle of conservation of mechanical energy can be applied. Therefore the magnitude of the velocity or speed of the object at position 2, 3, and 4 must be the same. However, if friction force is considered, the speed of the object at position 2, 3, and 4 will not be the same. This is because friction force is a nonconservative force. Since a friction force is always arised to resist the motion of an object in both positive and negative direction along the same path, the work of a friction force cannot be expressed in form of potential energy change. In other words, the work of friction force does not depend on the sense of motion and the work of friction force depends only on the path of motion followed  by the application of the friction force. Therefore the sum of the related mechanical energy of the object does not remain constant. The total mechanical energy is reduced and part of the mechanical energy is transformed by the friction force into heat in form of thermal energy. Although the sum of the mechanical energy is reduced, the total energy of the system remains constant, that is the sum of the mechanical energy and thermal energy due to the motion of the object is a constant. There are also other forms of energy, for example electric energy, chemical energy, etc. When all forms of energy are considered, the principle of convservation of energy can then be valid under all conditions for any system.

Motion under Conservative Central Force

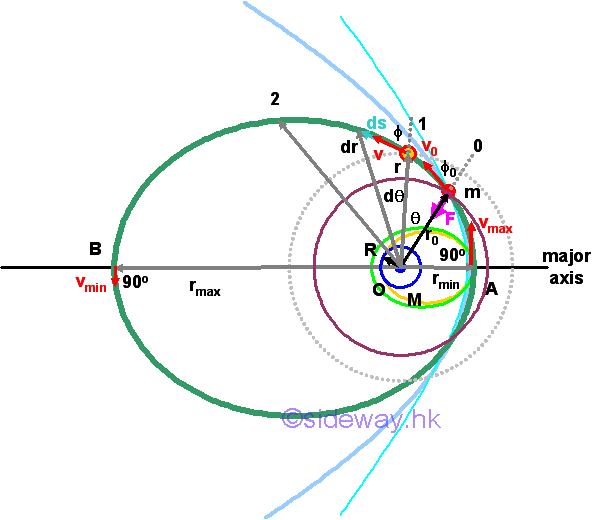
The free motion of an object under conservative central force, e.g. gravitational force of the Earth, depends on the velocity of the object with respect to the origin of the force center.In other words, the free flight trajectory of an object can be determined by the instantaneous velocity of the object with respect to the centre of gravitational force.

By the principle of conservation of angular momentum under a central force, the radial radius and the velocity of the object under free flight are related mathematically. Therefore the maximum and minimum values of radii and velocities can also be formulated accordingly.

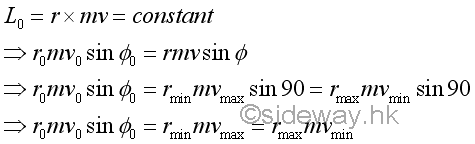
By the principle of conservation of mechanical energy under a conservative force, the radial radius and the velocity of the object under free flight can also be related mathematically. Therefore the maximum and minimum values of radii and velocities can also be formulated accordingly.

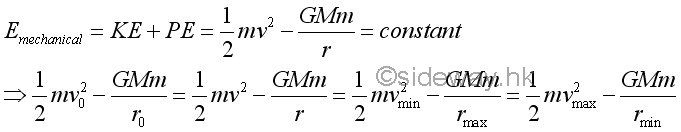
With two equations and two unknowns, the instantaneous velocity of the object can be eliminated and any interested radius can be obtained by setting the angle to the corresponding values. For example, the maximum and minimum radii can be obtained by making ϕ equals to 90o. Imply