Internal Forces in Beams

The shearing forces and bending moments in a statically determinate beam can be determined by the equilibrium equations. Using the standard convention, the distribution of internal forces in a beam can be represented graphically by plotting the values of shear or bending moment against the distance from one end of the beam.

Shear and Bending Moment Diagrams

Internal Forces in a Cantilever Beam

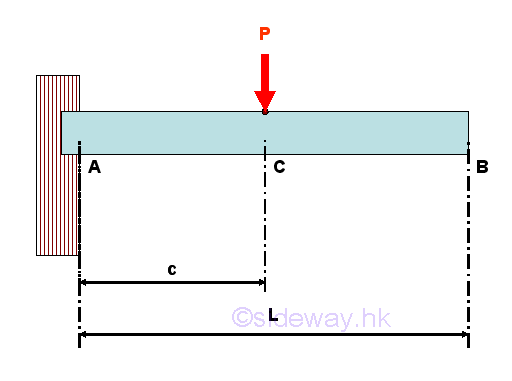
For example, consider a simple cantilevel beam with one applied load applied around the middle of the beam. The free-body diagram of the entire beam is

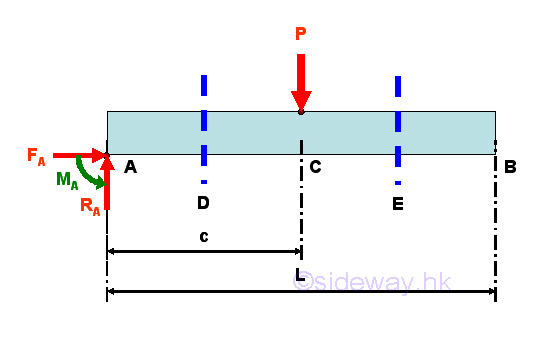
The reactions at the fixed support can be determined by the equilibrium equations.

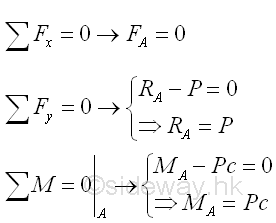
Internal forces can be determined by dividing the beam into two separated free body. Selecting a point D between A and C, i.e. A<D<C

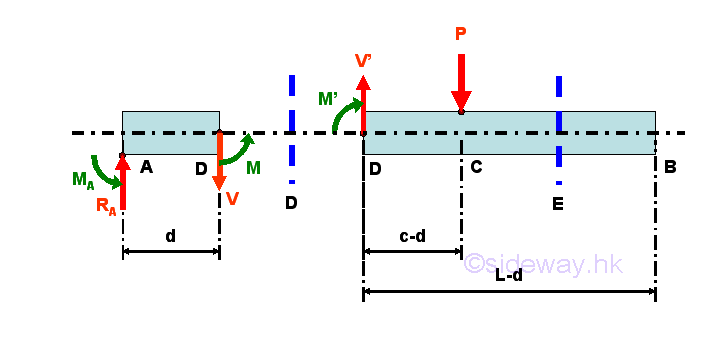
Consider the member section AD of length d, the internal forces at point D are

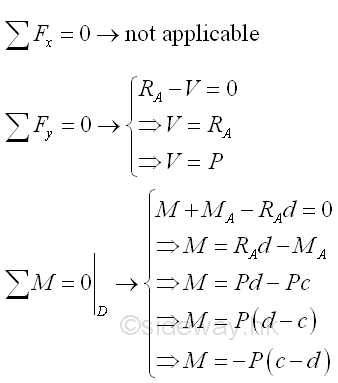
Point D is a random point between A and C. The shear force V is a constant and is equal to P between point A and point D. And bending moment M is a linear function of point D. Therefore bending moment M=-Pc at point A and bending moment M=0 at point C.

Selecting another point E between C and B, i.e. C<E<B

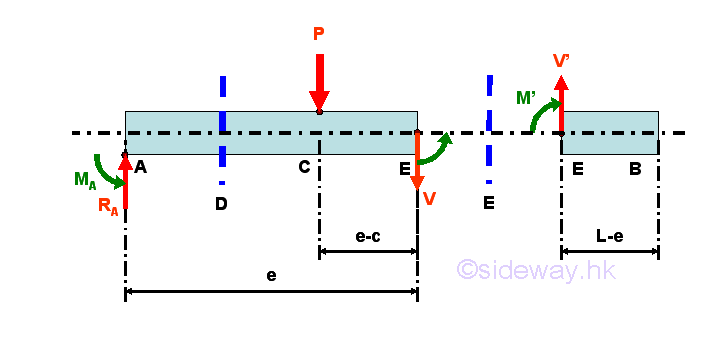
Consider the member section EB of length L-e, the internal forces at point E are

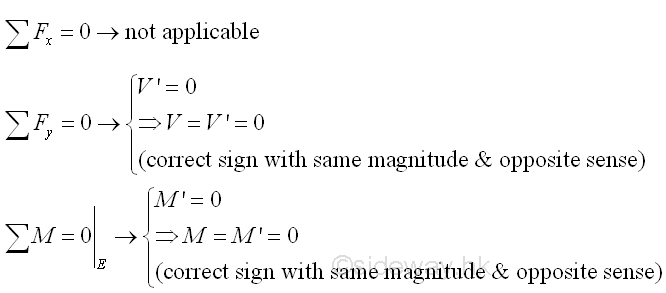
Point E is a random point between C and B. Both the shear force V and bending moment M is equal to zero between point C and point B.

Shear Diagram

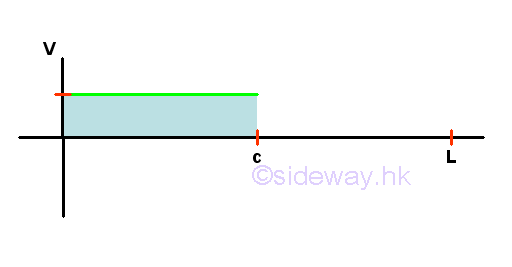
Bending Moment Diagram

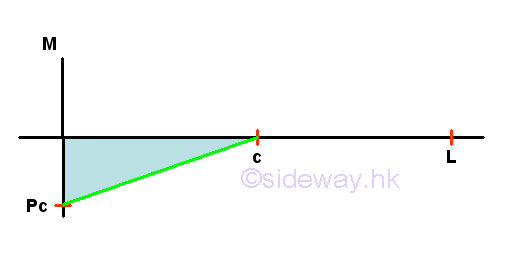
Internal Forces in a Simply Supported Beam

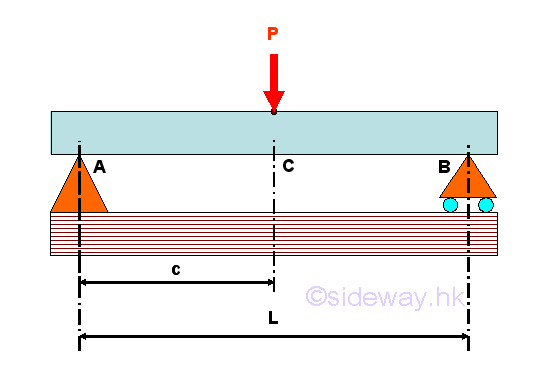
For example, consider a simply supported beam with one applied load applied around the middle of the beam. The free-body diagram of the entire beam is

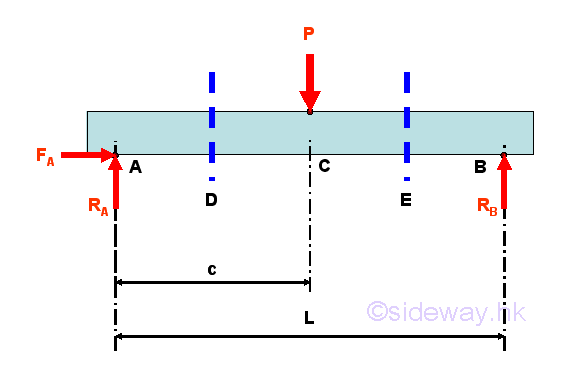
The reactions at the hinged and roller supports can be determined by the equilibrium equations.

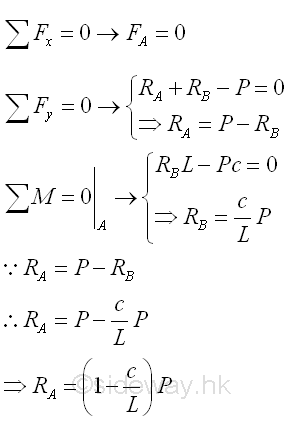
Internal forces can be determined by dividing the beam into two separated free body. Selecting a point D between A and C, i.e. A<D<C

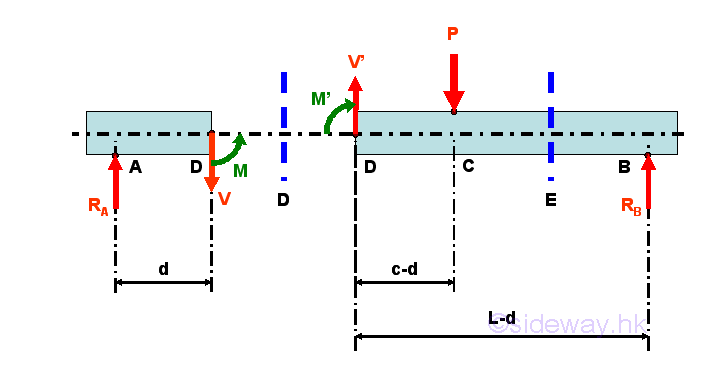
Consider the member section AD of length d, the internal forces at point D are

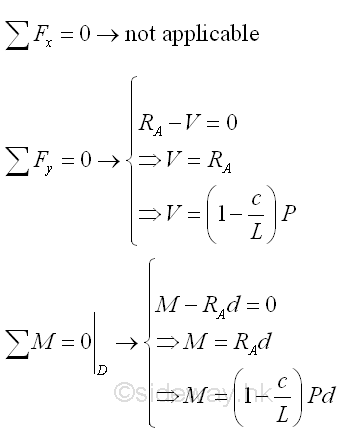
Point D is a random point between A and C. The shear force V is a constant and is equal to (1-c/L)P between point A and point C. And bending moment M is a linear function of point D. Therefore bending moment M=0 at point A and bending moment M=(1-c/L)Pc at point C.

Selecting another point E between C and B, i.e. C<E<B

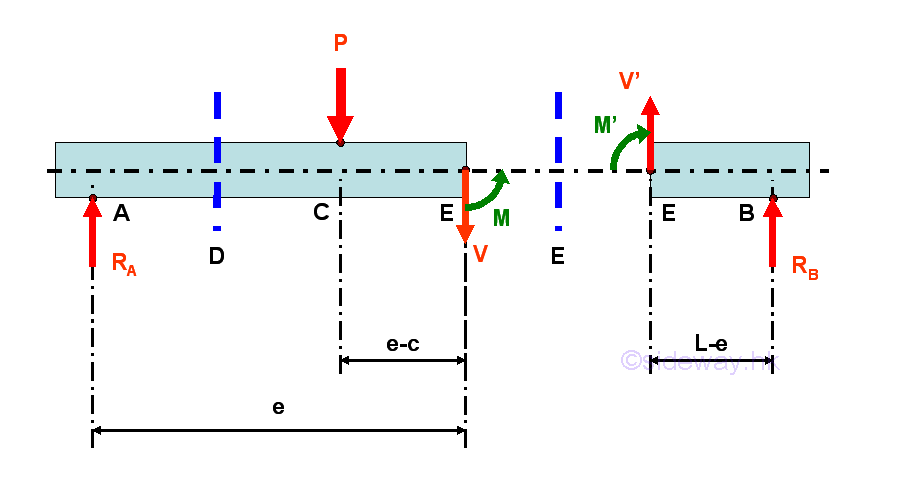
Consider the member section EB of length L-e, the internal forces at point E are

Point E is a random point between C and B. The shear force V is a constant and is equal to -(c/L)P between point C and point B. And bending moment M is a linear function of point E. Therefore bending moment M=(1-c/L)Pc at point C and bending moment M=0 at point B

Shear Diagram

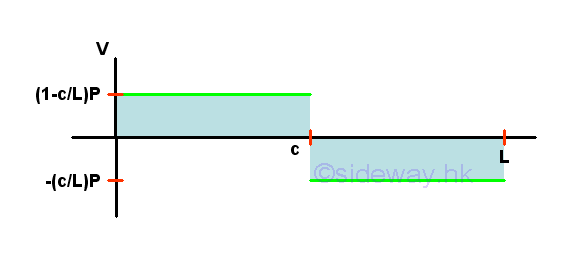
Bending Moment Diagram

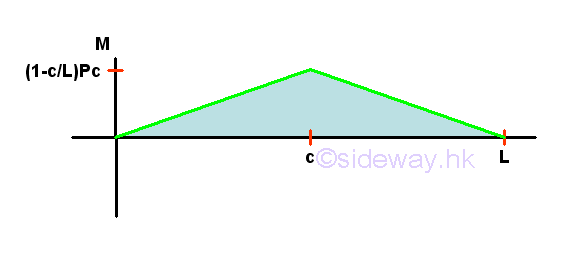
Internal Forces in a Overhanging Beam

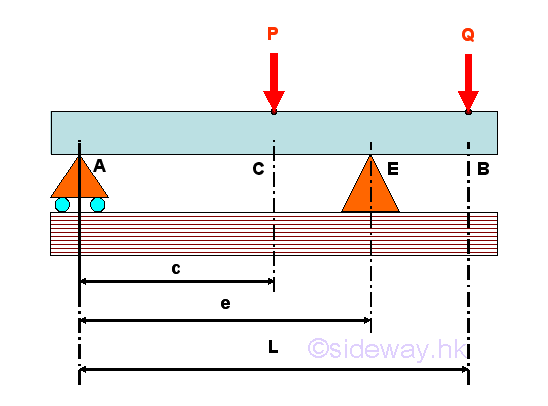
For example, consider a overhanging beam with two applied load applied around the middle and the free end of the beam. The free-body diagram of the entire beam is

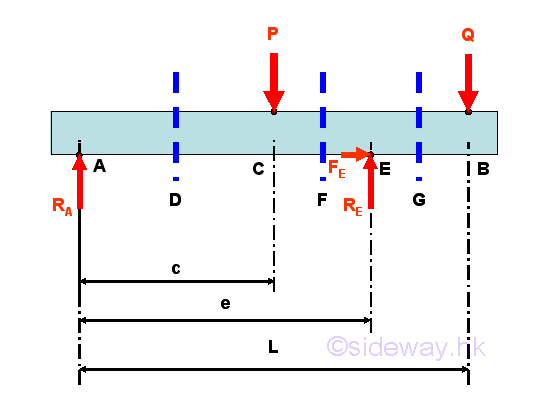
The reactions at the roller and hinged supports can be determined by the equilibrium equations.

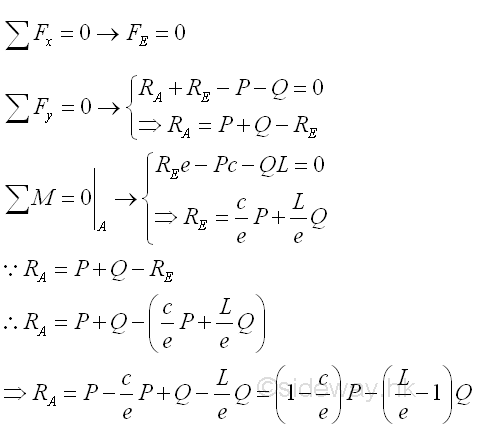
Internal forces can be determined by dividing the beam into two separated free body. Selecting a point D between A and C, i.e. A<D<C

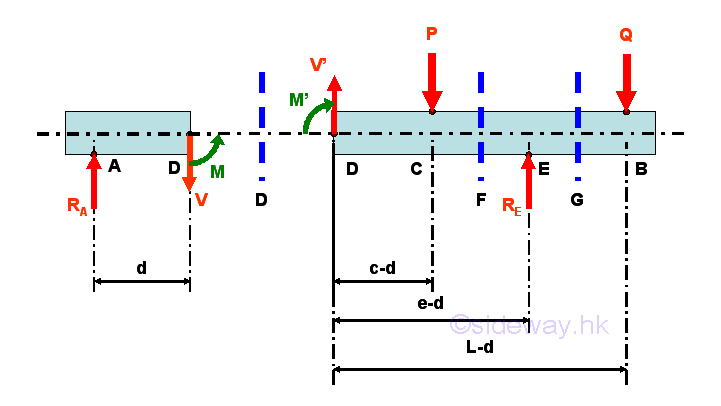
Consider the member section AD of length d, the internal forces at point D are

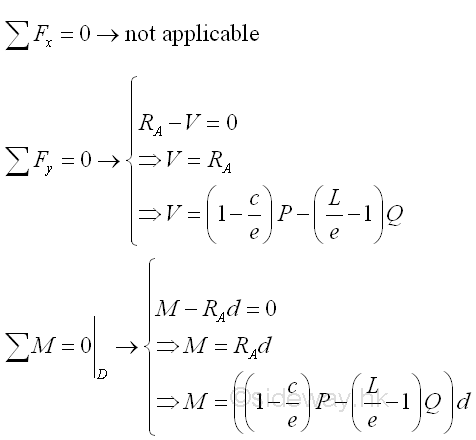
Point D is a random point between A and C. The shear force V is a constant and is equal to ((1-c/e)P-(L/e-1)Q) between point A and point C. And bending moment M is a linear function of point D. Therefore bending moment M=0 at point A and bending moment M=((1-c/e)P-(L/e-1)Q)c at point C.

Selecting another point F between C and E, i.e. C<F<E

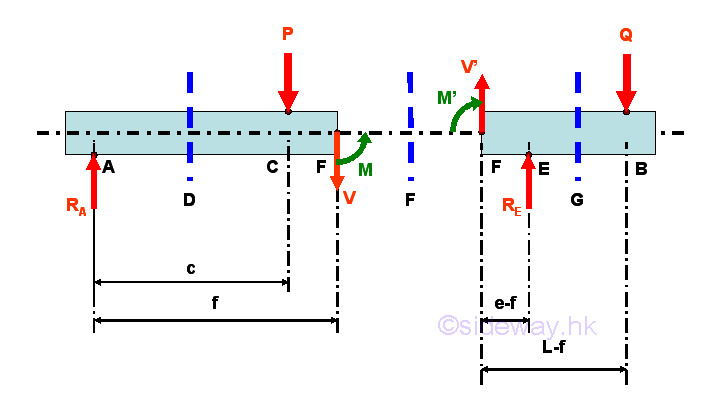
Consider the member section AF of length f, the internal forces at point F are

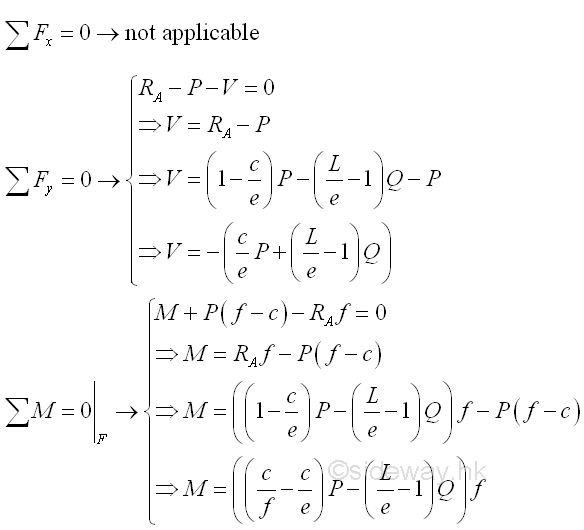
Point F is a random point between C and E. The shear force V is a constant and is equal to (-(c/e)P-(L/e-1)Q) between point C and point E. And bending moment M is a linear function of point F. Therefore bending moment M=((1-c/e)P-(L/e-1)Q)c at point C and bending moment M=-Q(L-e) at point E.

Selecting another point G between E and B, i.e. E<G<B

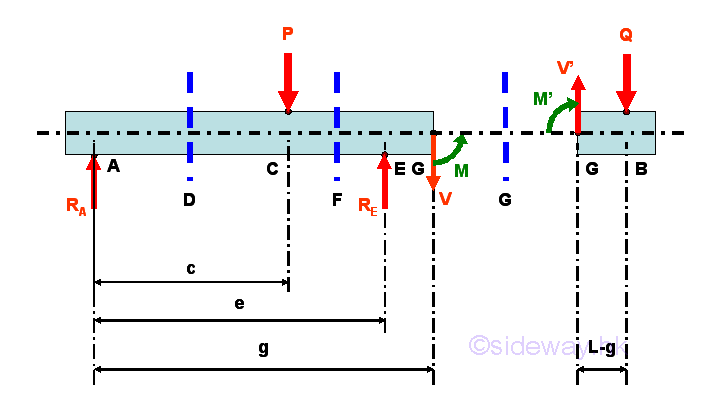
Consider the member section GB of length L-g, the internal forces at point G are

Point G is a random point between E and B. The shear force V is a constant and is equal to Q between point E and point G. And bending moment M is a linear function of point G. Therefore bending moment M=-Q(L-e) at point E and bending moment M=0 at point B.

Assumption for Shear and Bending Moment Diagrams

Since length L is greater than length e, the reaction force RA at point A may be negative if load Q term is greater than load P term. For normal practical applications, the reaction force RA at point A is usually pointing upward. Therefore, the reaction force RA at point A is assumed positive in plotting the shear and bending moment diagrams.

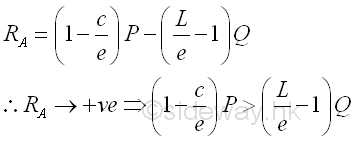
Shear Diagram

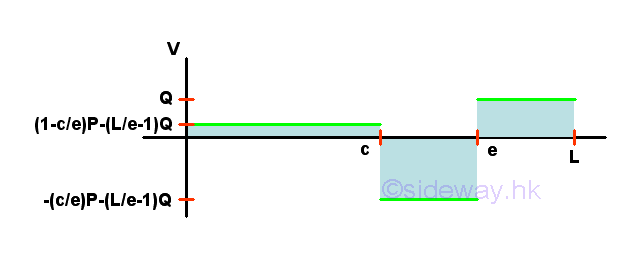
Bending Moment Diagram