Bounded Area by Functions

Bounded area under a function or bounded area under a curve is the signed area between the curve and the axis over the closed interval [a,b]. In general, the net signed area of the curve bounded by the curve of function f(x) and the x-axis over the closed interval [a,b] by definite integral is

The net signed bounded area is the summation of all positive and negative infinitesimal elements.  And therefore for problems of calculating the total bounded area of a function or concerning with the sign of the infinitesimal elements, the shape of the curve should be determined before applying the method of integration.

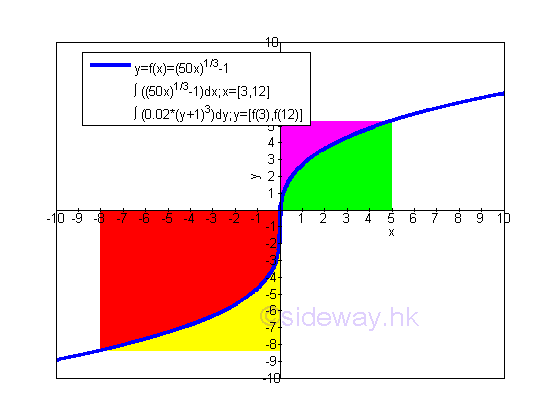
Depending on the arrangement of a function on the graph, there are two appraoches to calculate the bounded area between the curve and the axis. For bounded areas relatived to x axis, the bounded areas can be summed horzontally.  For bounded areas relatived to y axis, the bounded areas can be summed vertically. 

Bounded Area between Curves 

Unlike the concept of bounded area under curve, the bounded area by the curves of functions should always be positive and is equal to the total bounded area by curves of functions over the closed interval [a,b]. In order to obtain a positive area, the bounded area is always obtained by the function with larger value minus the function with smaller value. Therefore the shape of curves over the closed interval [a,b] should also be determined in order to identify all bounded areas before applying the method of integration.

In general, when summing the infinitesimal area elements horizontally, the bounded area should be determined by the upper function minus the lower function within the region.

And when summing the infinitesimal area elements vertically, the bounded area should be determined by the right function minus the left function within the region.

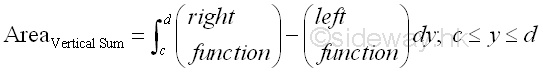
Bounded Area between curves by Horizontal  Approach or Vertical Approach:

Since the bounded area is bounded by curves of function, in some cases, the bounded area between curves can be obtained by either the horizontal sum or  vertical sum approaches. For example, the two curves of two monotonically increasing functions f(x) and h(x) forms two seperated regions of bounded area within a closed interval.

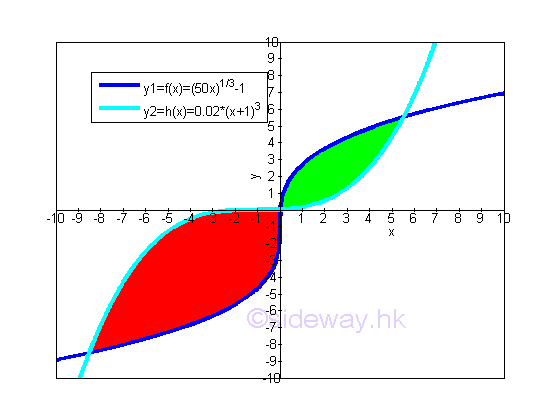
The closed intervals of the two regions of bounded areas are equal to the intersections of curves.  imply

The total bounded area between curves obtained by the horizontal sum approach is equal to the sum of the two regions of bounded areas. Imply

Since the bounded area is bounded by the two curves of two monotonically increasing functions f(x) and h(x), the total bounded area of the two seperated regions of bounded area within a closed interval can also be obtained by the vertical sum approach. The transformation of the two functions is

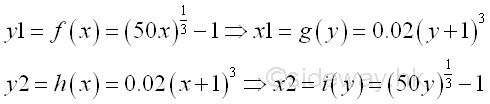
The bounded areas bounded by the two curves of two monotonically increasing functions g(x) and i(x) is

The total bounded area between curves obtained by the vertical sum approach is equal to the sum of the two regions of bounded areas. Imply

The total bounded area between curves obtained by the vertical sum approach is equal to the total bounded area between curves obtained by the horizontal sum approach. Because of the  summing method is changed from horizontal to vertical, the larger function in horizontal approach is also changed to the larger function in vertical approach accordingly. And therefore the larger function is highly depending on the domain and range used in the integration process.

Bounded Area between curves by Horizontal Approach:

In most cases, the approach used to obtaining total bounded area between curves is limited by the shapes of curves and the bounding curves. For example, if the range in x domain is changed to [-6,0.0213], the total bounded area of the curves of functions f(x) and h(x) on the closed interval [-6,0.0213] becomes.

The easiest way to calculate the bounded area between curves is the horizontal sum approach. imply

Bounded Area between curves by Vertical Approach:

And in some cases, an additional curve, e.g. y>=-6 can be used as additional constrain with the range in x domain, e.g. [-8.5262,0.0213]. The total bounded area of the curves of functions f(x), h(x) and f(x)>=-6 on the closed interval [-8.5262,0.0213] becomes.

Since y should be greater or equal to -6, the bounded area in x domain and  y domain is

The easiest way to calculate the bounded area between curves is the vertical sum approach. imply

Bounded Area between curves by Horizontal  and Vertical Approaches:

But in some cases, when an additional curve, e.g. y>=-6 is used as additional constrain with a shorter range in x domain, e.g. [-6,0.0213]. the total bounded area of the curves of functions f(x), h(x) and f(x)>=-6 on the closed interval [-6,0.0213] becomes.

One way to calculate the bounded area between curves is using a vertical sum approach minus a horizontal sum approach. imply

Similarly the bounded area between curves can also be obtained by a horizontal sum approach minus a vertical sum approach.

Another way to calculate the bounded area between curves is using  horizontal sum approach only by dividing the bounded area into two regions of bounded areas. The intervals of two regions are

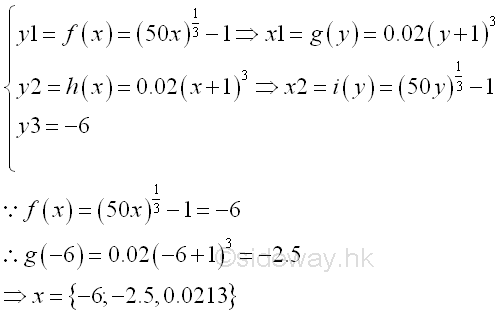
Therefore the bounded area between curves can also be obtained by adding two region of horizontal sum approach. Imply

Similarly the bounded area between curves can also be obtained by adding two region of vertical sum approach.