Content
Slope of Tangent Line
Curve Sketching
Curve Sketching Problem
Relative Extreme Value
Relative Maximum Problem
Relative Minimum Problem
Slope of Tangent Line
Both the first derivative and second derivative of a function can provide the gradient information about steepness of the graph of the function. The common applications of slope of tangent are curve sketching and relative extreme value finding.
Curve Sketching
Before sketching the curve of the function, some important points should be found first. The first type of points are critical points at which the derivative equals zero or does not exist. The second type of points are the stationary or turning points, they can be the position of points of inflexion, points of local minima, and points of local maxima. Another types of points are the y-intercept and x-intercepts.
After finding these importants positions, the next step is to carry out a gradient or slope analysis for the basic sketching of the curve. Finally the curve can be drafted according to the acquired information.
Curve Sketching Problem
The shape of the curve of a function y=x3-7x2+14x-8 is:
-
Calculate y-intercept: at x=0 imply y=-8
-
Calculatex-intercept let y=0, imply:
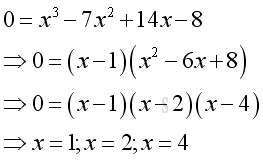
-
Compute the first derivative of function y is
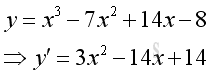
-
Find critical points where first derivative equals to zero or do not exist, imply:
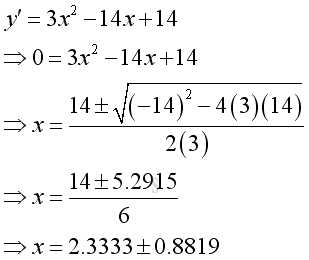
-
Determine the stationary points by subsituting x into y are:
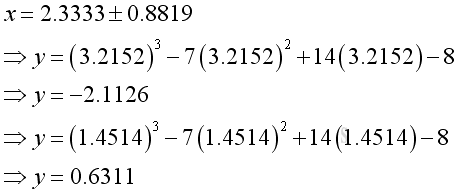
-
Use the first derivative to analysis the slope or gradient of the curve:
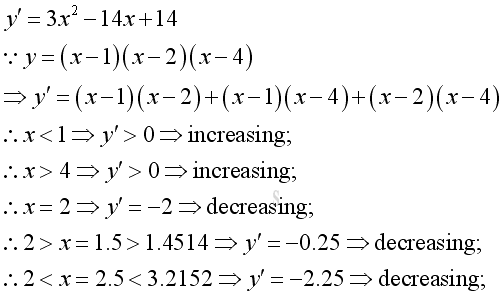
-
Use the second derivative to analysis the slope or gradient of the curve according to the stationary points:

-
Sketch the curve
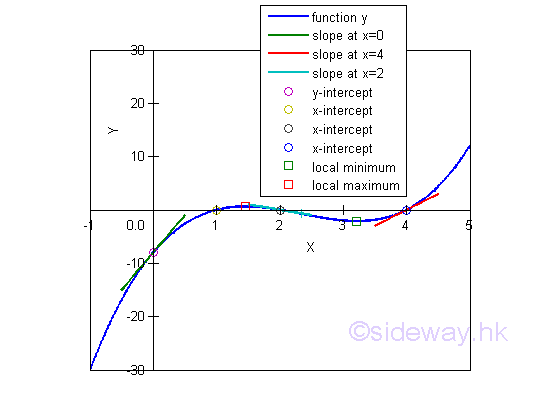
Relative Extreme Value
Optimization is one of the most important processes in industry. When interpreting the design criteria as constraints, a design problem can then be modelled, analyzed and evaluated using a mathematical model. In general, optimization is the process of finding maximum or minimum values of a task. When expressing requirements as a function, the optimization processes becomes a finding maximum or minimum value problem.
Relative Maximum Problem
Given a sheet of metal with size 4x6 to build a retangular container with the width equal half of length. The maximum volume is:
In order to make the retangular container, four square corners of lenght x are cut away.
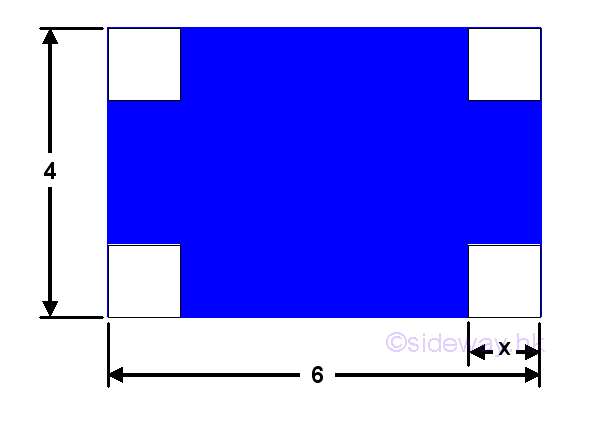
According to the criteria, the value of x is limited in the domain [0,2]. Let x be the height, then width equals to 4-2x and length equals to 6-2x. The problem can be modelled as:
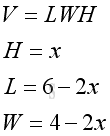
The volume of the retangular container is:
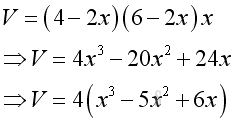
To determine the maximum volume of a rectangular container from the metal sheet, the volume can be evaluated with respect to x, that is to analyze by means of differentiation.
Take the first derivative of the volume function with respect to x equals to zero to determine the stationary points:
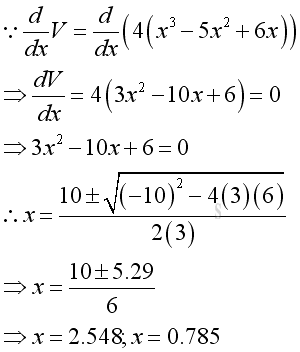
Since x can not be equal to 2.548 because of larger than 2, x can be 0.785 only.
Find the value of the second derivative at the stationary point,
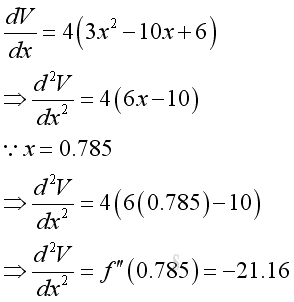
Since the second derivative less than zero, the position of x=0.785 is the largest volume. That is
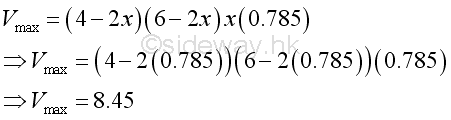
Graphically,
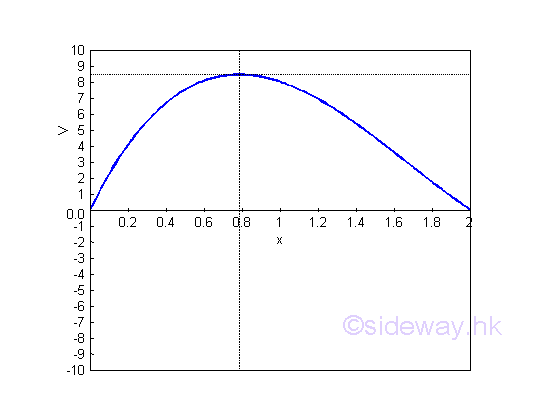
Relative Minimum Problem
Given a sheet metal to build a retangular container with height 0.785 and volume 8.45. The minimum material used is.
In order to make the retangular container, four square corners of lenght x are cut away.
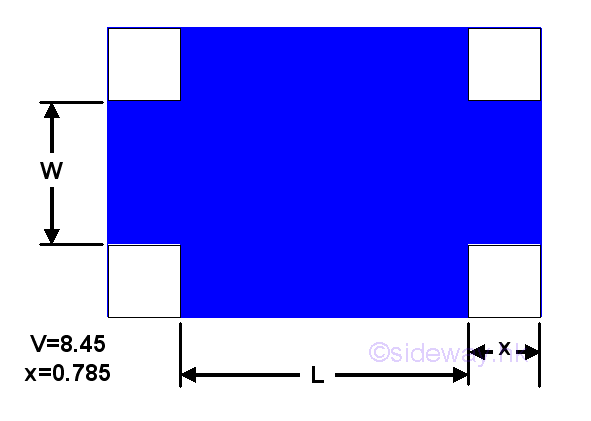
According to the criteria, given volume is 8.45 and the height of the container is 0.785. Let W be the width of the rectangular container, L be the length of rectangular container. The problem can be modelled as:.
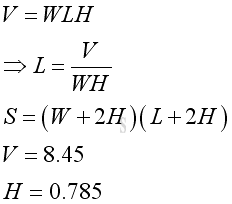
Let x be the width W of the rectangular container. The surface area of the metal sheet for the retangular container in terms of x is:

Therefore, the minimum dimension of the metal sheet is transformed to a function of the width of the rectangular container. The minimum dimension of the metal sheet can therefore can be evaluated with respect to x, the width of the rectangular container that is to analyze by means of differentiation.
Take the first derivative of the surface area function with respect to x equals to zero to determine the stationary points:
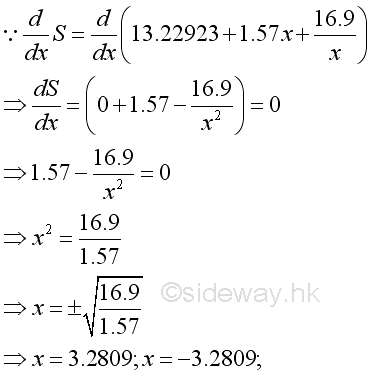
Since x can not be equal to -3.2809, a negative number, x can be 3.2809 only.
Find the value of the second derivative at the stationary point,

Since the second derivative greater than zero, the position of x=3.2809 is the minimum surface area of the metal sheet. That is
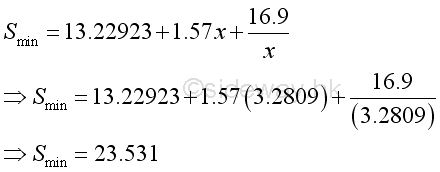
Graphically,
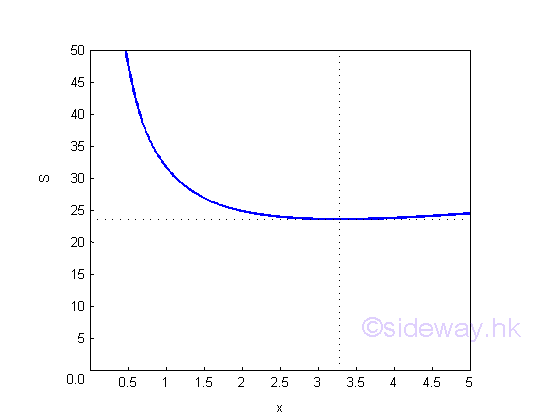
The dimension of the metal sheet is,

The minimum dimension of the metal sheet is a square metal sheet of dimension, 4.8509x4.8509=23.531. The material usage for building the rectangular container is less than the 4x6 metal sheet.
The maximum value problem of the first example is the optimization of the usage of available material for the application of designing a rectangular container, while the minumum value porblem of this example is the optimization of the material usage in a required rectangular container design.
©sideway
ID: 110900027 Last Updated: 9/29/2001 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Travel Singapore Sight Mandai(last updated On 12/8/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/7/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 24
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
