Content
Acoustic Wave Propagation
Acoustic Propagation Properties
Linearized
Acoustic
Wave Equation, 1D
Speed of Acoustic Wave Propagation
Wave Equation, 1D
Acoustic Wave Propagation
Based on linear acoustic, assuming the
cross-section area equals to A and no mass is entering or leaving the system due to the acoustic
disturbance, the wave propagation can be represented by following figure:

where, at ambient environment
and at acoustic disturbance state:
 and,
and,

where,
properties of acoustic disturbance:

where,
properties at wavefront:

Acoustic Propagation Properties
Since the acoustic pressure variations is much smaller than the ambient
pressure, the total pressure approximately equals to the ambient pressure.
Similarly, the acoustic density variations is also much smaller than the
ambient medium density, the total medium density approximately equals to the
ambient medium density. For a quiescent medium, the initial medium velocity equals to
zero, therefore the total velocity equals to the acoustic velocity variations.
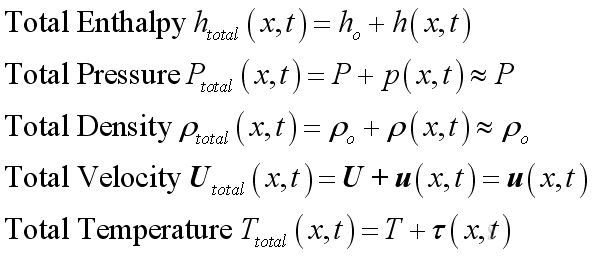
Besides, for a homogenous quiescent medium, the initial medium velocity, the
ambient pressure and the ambient medium density are constant and independent of
time and position. Therefore:

Linearized Acoustic Wave Equation, 1D
Since both u
, ρ are very small
when comparing with ρo and they are a
function of time and position, equations can be linearized by neglecting
second and higher order terms.
Substitute.variables
approximation into continuity equation
and linearize the equation by neglecting second and higher order terms, then:

The time derivative of the equation is

Substitute.variable
approximations into equation
of motion and linearize the equation by neglecting second and higher order terms, then:
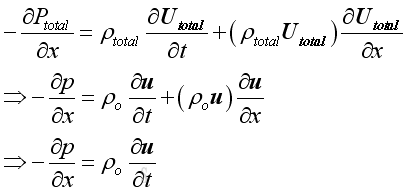
The position derivative of the equation is
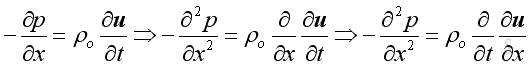
Therefore, equate the conservation of mass and conservation of momentum, then:
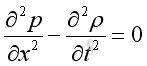
To simplify the equation, the equation of state is applied and to make the equation more practical, the equation is expressed in term of the fluctuating pressure, which can be measured easily. Then
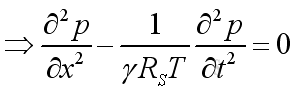
Speed of Acoustic Wave Propagation
For a control volume, when reducing the control volume to the medium at the wavefront of acoustic wave propagation, from the principle of mass conservation, the mass of medium in the control volume should be constant.
Assume c
is the speed of wavefront propagation and propagates away from the source, and Δu is the acoustic velocity
fluctuation, since the fluctuation is a relative velocity to the wave
propagation, the net medium velocity is
c-Δu at the acoustic source side. Then
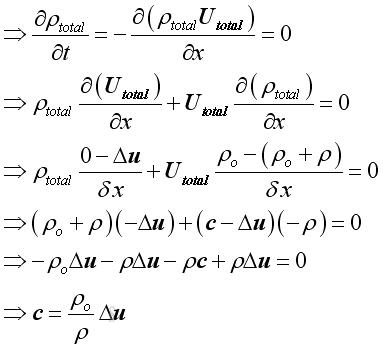
Alternately, the continuity equation can be expressed as the
net instantaneous mass flow into and out of the control volume to be equal. Then
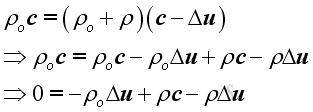
Since c is much greater than Δu, therefore:
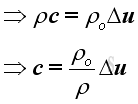
Similarly, for the same control volume, from principle of energy conservation, the energy of medium in the control volume should be constant.
Assume Δh
is the acoustic enthalpy variations of the medium in the control volume. Since
ρtotalutotal
is not equal to zero and conservation of mass, by neglecting second
order small term. Then:
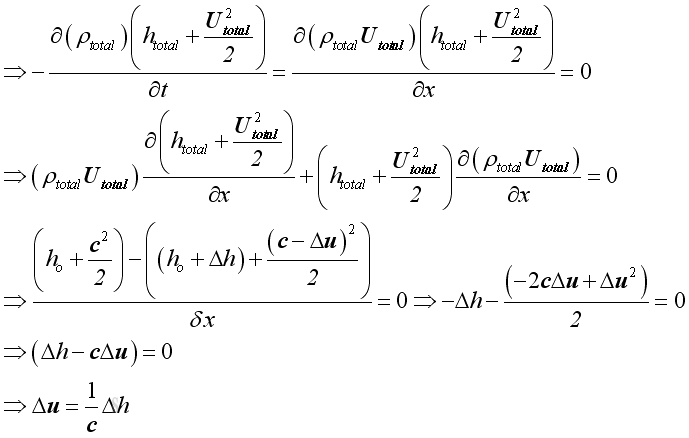
Alternately, the conservation of energy can be expressed as the net instantaneous energy flow into and out of the control volume to be equal. Then
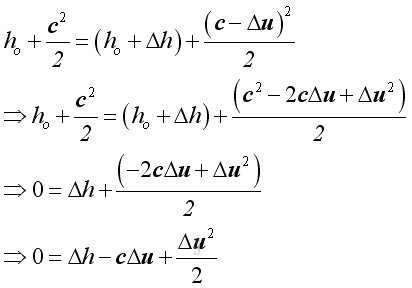
Neglecting second order small term. Then
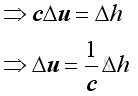
Equating mass conservation and energy conservation. Then

The acoustic disturbance is small and can be assumed as an isentropic process. Imply
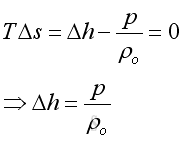
Substitute Δh into the equation of wave propagation, Imply

Since both ρ and p are the small acoustic fluctuation, and under isentropic process, imply
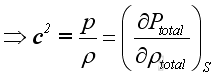
For an isentropic process, imply
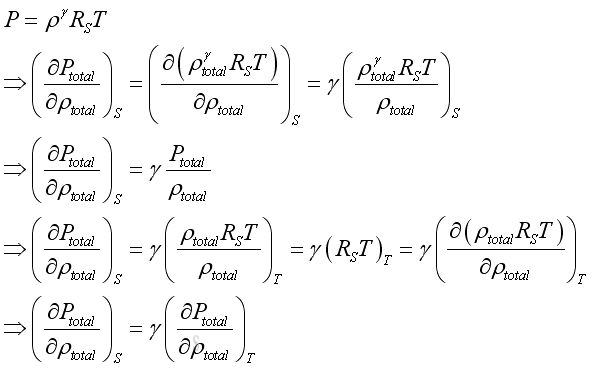
Substitute into the equation of wave propagation, Imply

Wave Equation, 1D
Substitute the speed of wave propagation into the wave equation, Imply
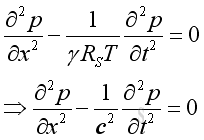
©sideway
ID: 100900020 Last Updated: 9/17/2010 Revision: 1 Ref:
References
- Michael P. Norton; Denis G. Karczub,, 2003, Fundamentals of Noise and Vibration Analysis for Engieer
- G. Porges, 1977, Applied Acoustics
- Douglas D. Reynolds, 1981, Engineering Principles of Acoustics:; Noise and Vibration Control
- Conrad J. Hemond, 1983, Engineering Acoustics & Noise Control
- F. Fahy, 2001, Foundations of Engineering Acoustics
- D.A. Biew; C.H. Hansen, 1996, Engineering Noise Control: Theory and Practice
Latest Updated Links
- Philips CL400 Ceiling Light 13W(last updated On 10/30/2025)
- Ikea TISKEN basket(last updated On 10/29/2025)
- Ikea TISKEN towel rack(last updated On 10/28/2025)
- Ikea REXBEGONIA mattress protector(last updated On 10/27/2025)
- Ikea KEJSAROLVON mattress protector(last updated On 10/26/2025)
- Ikea KVARNVEN ergonomic pillow(last updated On 10/25/2025)
- Ikea BRUKSVARA pocket prung mattress(last updated On 10/24/2025)
- Ikea VÅGSTRANDA pocket sprung mattress super firm(last updated On 10/23/2025)
- Ikea VITVAL underbed(last updated On 10/22/2025)
- Ikea SLÄKT bed frame with slatted bed base(last updated On 10/21/2025)
- ASUS TUF ESD-T1A External SSD Enclosure(last updated On 10/20/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 23![]()
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
